题目内容
【题目】数学活动课上，小颖同学用两块完全一样的透明等腰直角三角板ABC、DEF进行探究活动．
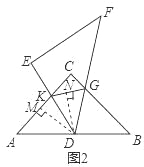
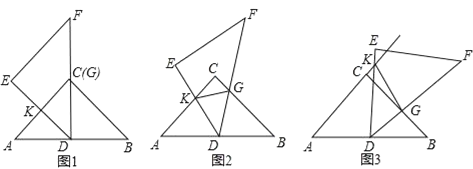
操作：使点D落在线段AB的中点处并使DF过点C(如图1)，然后将其绕点D顺时针旋转，直至点E落在AC的延长线上时结束操作，在此过程中，线段DE与AC或其延长线交于点K，线段BC与DF相交于点G(如图2，3)．
探究1：在图2中，求证：△ADK∽△BGD．
探究2：在图2中，求证：KD平分∠AKG．
探究3：
①在图3中，KD仍平分∠AKG吗？若平分，请加以证明；若不平分，请说明理由．
②在以上操作过程中，若设AC=BC=8，KG=x，△DKG的面积为y，请求出y与x的函数关系式，并直接写出x的取值范围．
【答案】探究1：证明见解析；探究2：证明见解析；探究3：y=2x，其中4≤x≤8
-8．
【解析】
试题探究1，根据△ABC、△DEF是等腰直角三角形可知∠KAD=∠KDG=∠DBG=45°，由三角形内角和定理可知∠KDA+∠BDG=135°．∠BDG+∠BGD=135°，故可得出△ADK∽△BGD；
探究2，根据△ADK∽△BGD可知
，再由点D是线段AB的中点得出BD=AD，故可得出△ADK∽△DCK，∠AKD=∠DKC，由此可得出结论；
探究3，①同探究1可得△ADK∽△BGD，同探究2可得，△ADK∽△DGK，故可得出结论；
②过点D作DM⊥AC于点M，DN⊥KG于点N，由①知线段KD平分∠AKG，故DM=DN．再由AC=BC=8，点D是线段AB的中点，∠KAD=45°，可知DM=DN=4．根据三角形的面积公式即可得出结论．
试题解析：探究1，
∵∠KAD=∠KDG=∠DBG=45°，
∴∠KDA+∠BDG=135°．
∵∠BDG+∠BGD=135°，
∴∠KDA=∠BGD，
∴△ADK∽△BGD；
探究2，∵△ADK∽△BGD，
∴，
∵点D是线段AB的中点，
∴BD=AD，
∴
，
∴
，
∵∠KAD=∠KDG=45°，
∴△ADK∽△DCK，
∴∠AKD=∠DKC，
∴KD平分∠AKG．
探究3，①KD仍平分∠AKG．
理由如下：
∵同探究1可得△ADK∽△BGD，
同探究2可得，△ADK∽△DGK，
∴∠AKD=∠DKG，
∴KD仍平分∠AKG；
②如图，过点D作DM⊥AC于点M，DN⊥KG于点N，
由①知线段KD平分∠AKG，
∴DM=DN．
∵AC=BC=8，点D是线段AB的中点，∠KAD=45°，
∴DM=DN=4．
∵KG=x，
∴S△DKG=y=
×4x=2x，
对于图3的情况同理可得y=2x，
综上所示，y=2x，其中4≤x≤8-8．
