Question

【题目】如图，D是△ABC的BC边上一点，连接AD，作△ABD的外接圆，将△ADC沿直线AD折叠，点C的对应点E落在上．

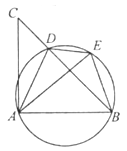
（1）求证：AE=AB；

（2）若∠CAB=90°，cos∠ADB=，BE=2，求BC的长．

Answer 1

【答案】（1）证明见解析；（2）BC=

【解析】分析: （1）由翻折的性质得出△ADE≌△ADC，根据全等三角形对应角相等，对应边相等得出∠AED=∠ACD，AE=AC，根据同弧所对的圆周角相等得出∠ABD=∠AED，根据等量代换得出∠ABD=∠ACD，根据等角对等边得出AB=AC，从而得出结论；

（2）如图，过点A作AH⊥BE于点H，根据等腰三角形的三线合一得出BH=EH=1，根据等腰三角形的性质及圆周角定理得出∠ABE=∠AEB=ADB，根据等角的同名三角函数值相等及余弦函数的定义得出BH∶AB = 1∶3,从而得出AC=AB=3，在Rt三角形ABC中，利用勾股定理得出BC的长.

详解:

（1）解 ：由题意得△ADE≌△ADC，

∴∠AED=∠ACD，AE=AC

∵∠ABD=∠AED，

∴∠ABD=∠ACD

∴AB=AC

∴AE=AB

（2）解 ：如图，过点A作AH⊥BE于点H

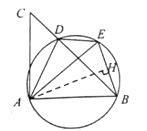
∵AB=AE，BE=2

∴BH=EH=1

∵∠ABE=∠AEB=ADB，cos∠ADB=

∴cos∠ABE=cos∠ADB=

∴ =

∴AC=AB=3

∵∠BAC=90°，AC=AB

∴BC=