题目内容
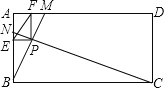
【题目】两块完全相同的直角三角形纸板ABC和DEF叠放,其中∠ABC=∠DEF=90°,点O为边BC和EF的交点.
(1)求证:△BOF≌△COE.
(2)若∠F=30°,AE=1,求OC的长.
【答案】(1)△BOF≌△COE(AAS),见解析;(2)OC=![]() ,见解析.
,见解析.
【解析】
(1)根据三角形全等的性质得到AB=DE,AC=DF,∠F=∠C,根据全等三角形的判定定理得到△BOF≌△COE(AAS);
(2)解直角三角形得到AC=2AE=2,求得CE=1,根据三角函数的定义即可得到结论.
解:(1)证明:∵△ABC≌△DEF,
∴AB=DE,AC=DF,∠F=∠C,
∴BF=CE,
在△BOF与△EOC中,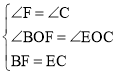 ,
,
∴△BOF≌△COE(AAS);
(2)解:∵∠ABC=∠DEF=90°,∠F=30°,AE=1,
∴∠C=∠F=30°,
∴AC=2AE=2,
∴CE=1,
∵∠CEO=∠DEO=90°,
∴OC=![]() =
=![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目