题目内容
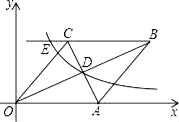
【题目】如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
①双曲线的解析式为y=![]() (x>0);
(x>0);
②E点的坐标是(5,8);
③sin∠COA=![]() ;
;
④AC+OB=12![]() .
.
其中正确的结论有 (填上序号).
【答案】③④.
【解析】
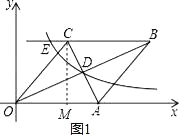
试题解析:①过点C作CM⊥x轴于点M,如图1所示.
∵OBAC=160,四边形OABC为菱形,
∴S△OCA=![]() OACM=
OACM=![]() OBAC=40,
OBAC=40,
∵A点的坐标为(10,0),
∴CM=8,OM=![]() =6,
=6,
∴点C(6,8),点B(16,8).
∵点D为线段OB的中点,
∴点D(8,4),
∵双曲线y=![]() (x>0)经过D点,
(x>0)经过D点,
∴k=8×4=32,
∴双曲线的解析式为y=![]() (x>0),
(x>0),
∴①不正确;
②∵点E在双曲线y=![]() (x>0)的图象上,且E点的纵坐标为8,
(x>0)的图象上,且E点的纵坐标为8,
∴32÷8=4,
∴点E(4,8),
∴②不正确;
③∵sin∠COA=![]() ,
,
∴③正确;
④在Rt△CMA中,CM=8,AM=OA-OM=10-6=4,
∴AC=![]() ,
,
∵OBAC=160,
∴OB=8![]() ,
,
∴AC+OB=12![]() .
.
∴④成立.
综上可知:③④成立.

练习册系列答案
相关题目