题目内容
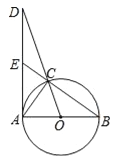
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
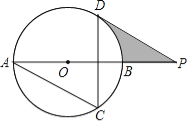
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
【答案】解:(1)证明:连接OD,
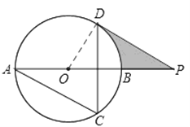
∵∠ACD=60°,
∴由圆周角定理得:∠AOD=2∠ACD=120°。
∴∠DOP=180°﹣120°=60°。
∵∠APD=30°,∴∠ODP=180°﹣30°﹣60°=90°。
∴OD⊥DP。
∵OD为半径,∴DP是⊙O切线。
(2)∵∠ODP=90°,∠P=30°,OD=3cm,
∴OP=6cm,由勾股定理得:DP=3![]() cm。
cm。
∴图中阴影部分的面积![]() 。
。
【解析】(1)连接OD,求出∠AOD,求出∠DOB,求出∠ODP,根据切线判定推出即可。
(2)求出OP、DP长,分别求出扇形DOB和△ODP面积,即可求出答案。

【题目】家庭过期药品属于“国家危险废物”处理不当将污染环境,危害健康.某市药监部门为了了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.
设计调查方式:
(1)有下列选取样本的方法
①在市中心某个居民区以家庭为单位随机抽取
②在全市医务工作者中以家庭为单位随机抽取
③在全市常住人口中以家庭为单位随机抽取.
其中最合理的一种是 .(只需填上正确答案的序号)
收集整理数据:
本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如下表:
处理 方式 | A 继续使用 | B 直接丢弃 | C 送回收点 | D 搁置家中 | E 卖给药贩 | F 直接焚烧 |
所占比例 | 8% | 51% | 10% | 20% | 6% | 5% |
描述数据:
(2)此次抽样的样本数为1000户家庭,请你绘制条形统计图描述各种处理过期药品方式的家庭数;

分析数据:
(3)根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是什么?说明你的理由;
(4)家庭过期药品的正确处理方式是送回收点,若该市有500万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收点.