题目内容
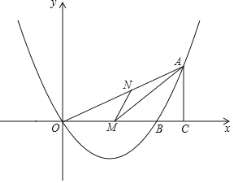
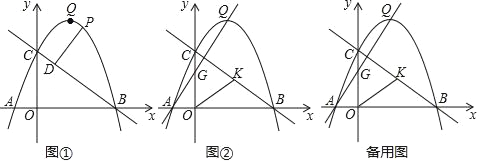
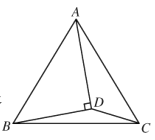
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 的内部,连接
的内部,连接![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为__________.
的长为__________.
【答案】9
【解析】
将△ADC绕点A顺时针旋转到△AEB,连接DE,根据旋转的性质证明△AED∽△ABC,利用相似三角形的性质结合∠ADB=90°推出∠EBD=90°,过点D作DF⊥AE,证明△EFD≌△EBD,得到BE=EF,根据![]() ,算出AF=3,在△AFD中,利用勾股定理算出AD,再在△ABD中利用勾股定理算出AC.
,算出AF=3,在△AFD中,利用勾股定理算出AD,再在△ABD中利用勾股定理算出AC.
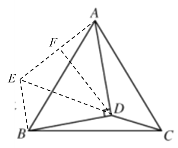
解:将△ADC绕点A顺时针旋转到△AEB,连接DE,
由题意可得:BD=6,∠ADC=∠AEB=2∠ABC,∠DAC=∠EAB,
∴∠EAD=∠BAC,
又∵AE=AD,AB=AC,
可知:△AED∽△ABC,
∴∠AED=∠ADE=∠BED=∠ABC=![]() ∠ADC=
∠ADC=![]() ∠AEB,
∠AEB,
∵∠ADB=∠ADE+∠BDE=90°,
∴∠BED+∠BDE=90°,
∴∠EBD=90°,
过点D作DF⊥AE,
∵∠BED=∠AED,
∴DB=DE=6,
在△EFD和△EBD中,
 ,
,
∴△EFD≌△EBD(AAS),
∴BE=EF,
∵![]() ,
,
设CD=x,
∴BE=EF=x,AD=AE=x+3,
∴AF=3,
在△AFD中,
AD=![]() ,
,
∴AC=AB=![]() .
.
故答案为:9.

练习册系列答案
相关题目