题目内容
【题目】已知：在平面直角坐标系中，抛物线
与
轴交于点
，
（点在点的右侧），点
为抛物线的顶点，点的纵坐标为-2．
（1）如图1，求此抛物线的解析式；
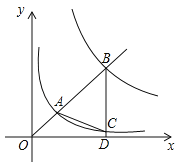
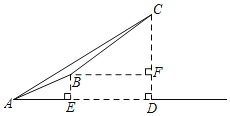
（2）如图2，点
是第一象限抛物线上一点，连接
，过点作
轴交于点
，设点的横坐标为
，
的长为
，求与的函数关系式（不要求写出自变量的取值范围）；
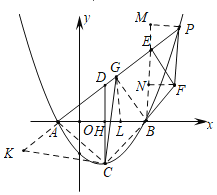
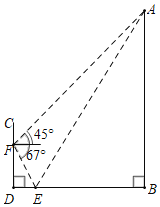
（3）如图3，在（2）的条件下，点
在
上，且
，点
的横坐标大于3，连接
，
，
，且
，过点作
交于点
，若
，求点的坐标．
【答案】（1）
；（2）
；（3）
【解析】
（1）将抛物线解析式化为顶点式可得y=a（x-1）2-4a，则C点为（1，-4a），再由-4a=-2即可求a的值，进而确定函数解析式；
（2）由已知分别求出点P和点A的坐标，可得AP的直线解析式，求出D点坐标则可求CD；
（3）设CD与x轴的交点为H，连接BE，由三角形中位线的性质可求BE=2（t-3）=2t-6；过点F作FN⊥BE于点N，过点P作PM⊥BE交BE的延长线于点M，可证明Rt△PME≌Rt△ENF（HL），从而推导出∠EPF=∠EFP=45°；过点C作CK⊥CG交PA的延长线于点K，连接AC、BC，能够进一步证明△ACK≌△BCG（SAS），得到∠KGB=90°；令AG=8m，则CG=
BG=6m，过点G作GL⊥x轴于点L，在Rt△ABG中，AG=10m=4，求出m值，利用等积法可求G点的坐标，再将G点坐标代入
，求出t，即可求出点P坐标.
解：（1）
，
顶点
的坐标为
，
点的纵坐标为
，
，
，
；
（2）点
的横坐标为
，
，
与
轴的交点为
，
，
设
的直线解析式为
，
则有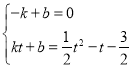
，
解得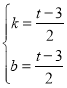
，
，
轴交于点
，
，
，
；
（3）如图：设
与轴的交点为
，连接
，
垂直平分
，
，
，
，
轴，
，
过点
作
于点
，过点作
交的延长线于点
，
，
，
，
，
，
，
，
，
过点作
交
的延长线于点
，连接
、
，
，
，
，
，
，
，
，
，
，
，
，
，
，
令
，则
，
，
，
，
，
过点
作
轴于点
，
在
中，
，
，
，
，
，
，
，
，
，
的解析式为，
，
，
，
．
