Question

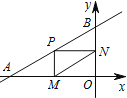
【题目】如图，直线与x轴、y轴分别交于A、B两点，点P是第二象限图象上一动点，PM⊥x轴于点M，PN⊥y轴于点N，连接MN，在点P的运动过程中，线段MN长度的最小值是________．

Answer 1

【答案】

【解析】

首先连接OP，易得四边形ONPM是矩形，即可得在Rt△AOB中，当OP⊥AB时OP最短，即MN最小，然后求出点A、B的坐标，再利用勾股定理与三角形的面积的求解，可求得MN的长．

解：如图，连接OP．

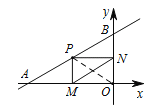
∵PM⊥x轴，PN⊥y轴，

∴∠PMO=∠MON=∠ONP=90°．

∴四边形ONPM是矩形．

∴OP=MN，

在Rt△AOB中，当OP⊥AB时OP最短，即MN最小．

直线中，令，则；令，则，

∴点A为（，0），点B为（0，2），

∴OA=，OB=2，

由勾股定理，得到AB=4，

由三角形的面积关系，则

，

即，

∴，

∴；

∴线段MN长度的最小值是；

故答案为：．