题目内容
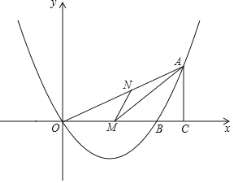
【题目】如图，已知二次函数 y＝ax2+bx 的图象与 x 轴交于点 O（0，0）和 点 B，抛物线的对称轴是直线 x＝3．点 A 是抛物线在第一象限上的一个动点， 过点 A 作 AC⊥x 轴，垂足为 C．S△AOB＝3S△ABC，AC2＝OCBC．
（1）求该二次函数的解析式；
（2）抛物线的对称轴与 x 轴交于点 M．连接 AM，点 N 是线段 OA 上的一点．当 ∠AMN＝∠AOM 时，求点 N 的坐标；
（3）点 P 是抛物线上的一个动点．点 Q 是 y 轴上的一动点．当以 A，B，P，Q 四个点为顶点的四边形为平行四边形时，直接写出点 P 坐标．
【答案】（1）y＝
； （2）
；（3）点 P 为（2，﹣2）或（﹣2，4）或（14，28）时以 A，B，P，Q 四个点为顶点 的四边形为平行四边形．
【解析】
（1）根据二次函数的对称性以及对称轴可以确定点B的坐标，然后结合题目中给到的面积关系
求出
,从而确定
,根据
求出
便可以确定点
的坐标，把点和
点代入二次函数解析式联立方程组便可求解；
（2）利用
可以证明
，结合相似的性质可以得到
,而
可以用勾股定理求出，
可以用两点间的距离公式求出，从而解出
,由于
在正比例函数
上，所以可以求出直线的解析式，设出的坐标，利用两点间的距离公式表示出，最后解出点的坐标；
（3）根据已知边
进行分类讨论，可能是平行四边形的对角线，也可能是四边形的边，然后再根据平行四边形的性质特点，即对角线交点即为对角线的中点，分别解出每种情况下点
的坐标；
（1）
函数对称轴为
，且与
轴交于
,则
又
点的坐标为：
将点，代入
，解得：
，
二次函数的解析式为：
（2） 抛物线的对称轴与
轴交于点
,
又
又
设直线的解析式为
，把代入得：
解得：
直线的解析式为
设
，
解得：
（不合题意，舍去）
当
时，
（3）设 
①当为平行四边形的边时，分为以下两种情况：
i：四边形
为平行四边形，
和
为对角线，
此时的中点横坐标为3，的中点横坐标为
解得：
ii: 四边形
为平行四边形，
和
为对角线
此时的中点横坐标为4，的中点横坐标为
解得：
②当为平行四边形的对角线时，
也为对角线
此时的中点横坐标为7，的中点横坐标为
解得：
综上所述，当以 A，B，P，Q 四个点为顶点的四边形为平行四边形时，点 P的坐标可能是：（2，﹣2）或（﹣2，4）或（14，28）；
