题目内容
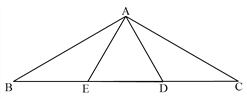
【题目】如图,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC.
(1)求证:△ABE≌△ACD;
(2)求证:△ADE是等边三角形.
【答案】见解析
【解析】试题分析:(1)利用两角及其夹边对应相等的两个三角形全(ASA)不难证明△ABE≌△ACD;由已知条件求出∠ADB =60°,∠AEC=60°,即可证明.
试题解析:
(1)证明∵AB=AC,
∴∠B=∠C,
∵AD⊥AB,AE⊥AC,
∴∠BAD=∠CAE =90°,
∴∠BAE=∠CAD,
∵在△ABE和△ACD中
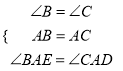 ,
,
∴△ABE≌△ACD (ASA);
(2)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
在△ABD中,∠B=30°,∠BAD =90°,
∴∠ADB =60°,
同理∠AEC=60°,
∴∠ADB=∠AEC=∠EAD=60°,
∴△ADE是等边三角形.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目