题目内容
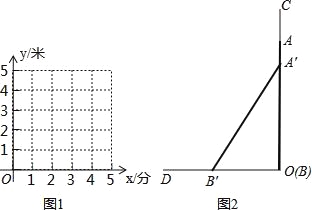
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.
(1)数轴上点A表示的数为
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S. ①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数为 .
②设点A的移动距离AA′=x.
ⅰ.当S=4时,x=;
ⅱ.D为线段AA′的中点,点E在线段OO′上,且OE= ![]() OO′,当点D,E所表示的数互为相反数时, x=
OO′,当点D,E所表示的数互为相反数时, x=
【答案】
(1)4
(2)6或2;![]() ;
;![]()
【解析】解:(1)∵长方形OABC的面积为12,OC边长为3, ∴OA=12÷3=4,
∴数轴上点A表示的数为4,
所以答案是:4. (2)①∵S恰好等于原长方形OABC面积的一半,
∴S=6,
∴O′A=6÷3=2,
当向左运动时,如图1,A′表示的数为2
当向右运动时,如图2,
∵O′A′=AO=4,
∴OA′=4+4﹣2=6,
∴A′表示的数为6,
所以答案是:6或2.②ⅰ.如图1,由题意得:COOA′=4,
∵CO=3,
∴OA′= ![]() ,
,
∴x=4﹣ ![]() =
= ![]() ,
,
所以答案是: ![]() ;
;
ⅱ.如图1,当原长方形OABC向左移动时,点D表示的数为 ![]() ,点E表示的数为
,点E表示的数为 ![]() ,
,
由题意可得方程:4﹣ ![]() x﹣
x﹣ ![]() x=0,
x=0,
解得:x= ![]() ,
,
如图2,当原长方形OABC向右移动时,点D,E表示的数都是正数,不符合题意.
【考点精析】通过灵活运用数轴和平移的性质,掌握数轴是规定了原点、正方向、单位长度的一条直线;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等即可以解答此题.

 名校课堂系列答案
名校课堂系列答案