题目内容
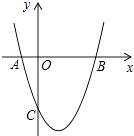
【题目】如图,直线L1:y=bx+c与抛物线L2:y=ax2的两个交点坐标分别为A(m,4),B(1,1). 
(1)求m的值;
(2)过动点P(n,0)且垂直于x轴的直线与L1 , L2的交点分别为C,D,当点C位于点D上方时,请直接写出n的取值范围.
【答案】
(1)解:把B(1,1)代入y=ax2得:a=1,
∴抛物线解析式为y=x2.
把A(m,4)代入y=x2得:4=m2,
∴m=±2.
∵点A在二象限,
∴m=﹣2
(2)解:观察函数图象可知:当﹣2<x<1时,直线在抛物线的上方,
∴n的取值范围为:﹣2<n<1
【解析】(1)根据点B的坐标利用二次函数图象上点的坐标特征即可求出a值,再将点A的坐标代入抛物线解析式中可求出m的值,结合点A在第二象限即可确定m的值;(2)根据两函数图象的上下位置关系即可得出:当﹣2<x<1时,直线在抛物线的上方,结合题意即可得出n的取值范围.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

练习册系列答案
相关题目