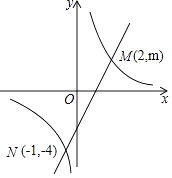Question

【题目】已知：关于x的方程x2﹣（m+2）x+m+1=0．
（1）求证：该方程总有实数根；
（2）若二次函数y=x2﹣（m+2）x+m+1（m＞0）与x轴交点为A，B（点A在点B的左边），且两交点间的距离是2，求二次函数的表达式；
（3）横、纵坐标都是整数的点叫做整点．
在（2）的条件下，垂直于y轴的直线y=n与抛物线交于点E，F．若抛物线在点E，F之间的部分与线段EF所围成的区域内（包括边界）恰有7个整点，结合函数的图象，直接写出n的取值范围．

Answer 1

【答案】
（1）

解：∵△=（m+2）2﹣4（m+1）=m2≥0，

∴不论m取何值，该方程总有实数根

（2）

解：由题意可知：y=x2﹣（m+2）x+m+1=（x﹣1）（x﹣m﹣1），

∴A（1，0），B（m+1，0）．

∵两交点间距离为2，

∴m+1﹣1=2．

∴m=2．

∴y=x2﹣4x+3

（3）

解：如图所示，

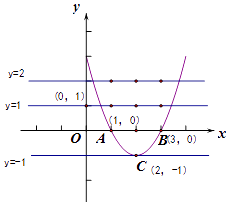
n的取值范围是：1≤n＜2

【解析】（1）根据关于x的方程x2﹣（m+2）x+m+1=0判别式的符号进行证明；（2）将已知函数解析式转化为两点式方程，求得点A、B的横坐标，然后结合已知条件求得m的值即可；（3）根据题意作出图形，结合图形直接写出n的取值范围．
【考点精析】解答此题的关键在于理解二次函数的概念的相关知识，掌握一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数，以及对二次函数的图象的理解，了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点．