题目内容
【题目】如图，矩形ABCD的顶点A在第一象限，AB∥x轴，AD∥y轴，且对角线的交点与原点O重合．在边AB从小于AD到大于AD的变化过程中，若矩形ABCD的周长始终保持不变，则经过动点A的反比例函数y= 
（k≠0）中k的值的变化情况是（ ） 
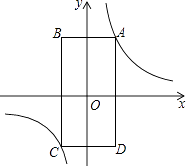
A.一直增大
B.一直减小
C.先增大后减小
D.先减小后增大
【答案】C
【解析】解：设矩形ABCD中，AB=2a，AD=2b． ∵矩形ABCD的周长始终保持不变，
∴2（2a+2b）=4（a+b）为定值，
∴a+b为定值．
∵矩形对角线的交点与原点O重合
∴k= 
AB AD=ab，
又∵a+b为定值时，当a=b时，ab最大，
∴在边AB从小于AD到大于AD的变化过程中，k的值先增大后减小．
故选：C．
设矩形ABCD中，AB=2a，AD=2b，由于矩形ABCD的周长始终保持不变，则a+b为定值．根据矩形对角线的交点与原点O重合及反比例函数比例系数k的几何意义可知k= AB AD=ab，再根据a+b一定时，当a=b时，ab最大可知在边AB从小于AD到大于AD的变化过程中，k的值先增大后减小．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：
时间x（天） | 1≤x＜50 | 50≤x≤90 |
售价（元/件） | x+40 | 90 |
每天销量（件） | 200﹣2x | |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
