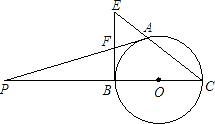Question

【题目】如图，在△ABC中，BD⊥AC于点D，CE⊥AB于点E，BD，CE交于点O，F为BC的中点，连接EF，DF，DE，则下列结论：①EF=DF；②ADAC=AEAB；③△DOE∽△COB；④若∠ABC=45°时，BE= FC． 其中正确的是（把所有正确结论的序号都选上）

Answer 1

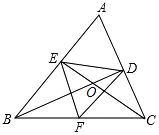
【答案】①②③④
【解析】解：∵BD⊥AC于点D，CE⊥AB于点E，F为BC的中点， ∴EF= BC，DF= BC，
∴EF=DF，故①正确；
∵∠BEC=∠BDC=90°，
∴B、C、D、E四点共圆，
由割线定理可知ADAC=AEAB，故②正确；
∵B、C、D、E四点共圆，
∴∠OED=∠OBC，∠ODE=∠OCB，
∴△DOE∽△COB，故③正确；
若∠ABC=45°，则△BEC为等腰直角三角形，
∴BC= BE，
∵F为BC中点，
∴FC= BC= BE，
∴BE= FC，故④正确；
所以答案是：①②③④．
【考点精析】通过灵活运用直角三角形斜边上的中线和相似三角形的判定与性质，掌握直角三角形斜边上的中线等于斜边的一半；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方即可以解答此题．