题目内容
【题目】已知a,b,c为正实数,且 ![]() ,则
,则 ![]() 的取值范围为 .
的取值范围为 .
【答案】[27,30]
【解析】解:∵ ![]() , ∴
, ∴ 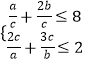 ,设x=
,设x= ![]() ,y=
,y= ![]() ,则有
,则有 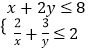 ,
,
∴ 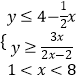 ,
,
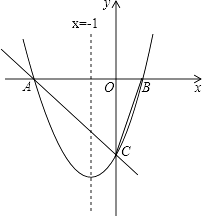
作出平面区域如图所示: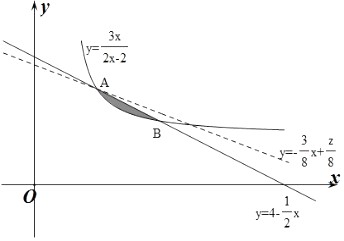
令z= ![]() =3x+8y,则y=﹣
=3x+8y,则y=﹣ ![]() +
+ ![]() ,
,
由图象可知当直线y=﹣ ![]() +
+ ![]() 经过点A时,截距最大,即z最大;
经过点A时,截距最大,即z最大;
当直线y=﹣ ![]() +
+ ![]() 与曲线y=
与曲线y= ![]() 相切时,截距最小,即z最小.
相切时,截距最小,即z最小.
解方程组  得A(2,3),∴z的最大值为3×2+8×3=30,
得A(2,3),∴z的最大值为3×2+8×3=30,
设直线y=﹣ ![]() +
+ ![]() 与曲线y=
与曲线y= ![]() 的切点为(x0 , y0),
的切点为(x0 , y0),
则( ![]() )′|
)′| ![]() =﹣
=﹣ ![]() ,即
,即 ![]() =﹣
=﹣ ![]() ,解得x0=3,
,解得x0=3,
∴切点坐标为(3, ![]() ),∴z的最小值为3×3+8×
),∴z的最小值为3×3+8× ![]() =27.
=27.
∴27≤z≤30,
所以答案是:[27,30].

练习册系列答案
相关题目