题目内容
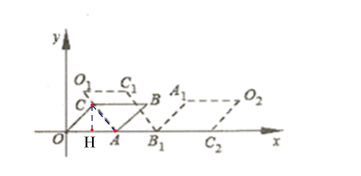
【题目】如图,在平面直角坐标系中.四边形![]() 是平行四边形,其中
是平行四边形,其中![]() 将
将![]() 在
在![]() 轴上顺时针翻滚.如:第一次翻滚得到
轴上顺时针翻滚.如:第一次翻滚得到![]() 第二次翻滚得到
第二次翻滚得到![]() ,···则第五次翻滚后,
,···则第五次翻滚后,![]() 点的对应点坐标为( )
点的对应点坐标为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】
![]() 在x轴上顺时针翻滚,四次一个循环,推出第五次翻滚后,点A的坐标,再利用平移的性质求出C的对应点坐标即可.
在x轴上顺时针翻滚,四次一个循环,推出第五次翻滚后,点A的坐标,再利用平移的性质求出C的对应点坐标即可.
连接AC,过点C作CH⊥OA于点H,
∵四边形OABC是平行四边形,A(2,0)、B(3,1),
∴C(1,1),
∴∠COA=45°,OC=AB=![]() ,
,
∴OH= OC÷![]() =1,
=1,
∴AH=2-1=1,
∴OA=AH,
∴OC=AC,
∴OAC是等腰直角三角形,
∴AC⊥OC,
∵![]() 在x轴上顺时针翻滚,四次一个循环,
在x轴上顺时针翻滚,四次一个循环,
∴第五次翻滚后点,A的坐标为(6+2![]() ,0),把点A向上平移
,0),把点A向上平移![]() 个单位得到点C,
个单位得到点C,
∴第五次翻滚后,C点的对应点坐标为![]() .
.
故选:A.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目