题目内容
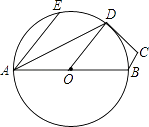
【题目】在![]() 中,
中,![]() 是
是![]() 的中线,
的中线,![]() 为
为![]() 的中点,过点
的中点,过点![]() 作
作![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() ,连接
,连接![]() .
.
(1)如图1,求证:四边形![]() 是平行四边形;
是平行四边形;


(2)如图2,若![]() ,请直接写出图中所有的等腰三角形,不需要证明.
,请直接写出图中所有的等腰三角形,不需要证明.
【答案】(1)见解析;(2)图中所有的等腰三角形为△ACE、△CDE、△BCF、△AEF.
【解析】
(1)根据AAS可证△AEF≌△DEC,可得AF=DC,结合条件,得AF=BD,AF∥BD,进而即可得到结论;
(2)根据直角三角形斜边上的中线等于斜边的一半,得△ACE、△CDE、△AEF是等腰三角形,由AD=FC,结合四边形![]() 是平行四边形,可得△BCF是等腰三角形.
是平行四边形,可得△BCF是等腰三角形.
(1)∵E是AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DCE,
在△AEF和△DEC中,
∵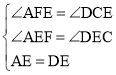 ,
,
∴△AEF≌△DEC(AAS),
∴AF=DC,
∵AD是△ABC的中线,
∴BD=DC,
∴AF=BD,
又∵AF∥BC,即AF∥BD,
∴四边形BDAF是平行四边形;
(2)∵∠ACD=90°,E是AD的中点,
∴CE=![]() AD=AE=DE,
AD=AE=DE,
∴△ACE和△CDE是等腰三角形,
由(1)得:△AEF≌△DEC,
∴FE=CE,
∴CE=![]() AD=AE=DE=FE,
AD=AE=DE=FE,
∴△AEF是等腰三角形,
∵四边形BDAF是平行四边形,
∴BF=AD=CF,
∴△BCF是等腰三角形,
综上所述:图中所有的等腰三角形为:△ACE、△CDE、△BCF、△AEF.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】[实际背景]预警方案确定:
设![]() ,如果当月
,如果当月![]() 则下个月要采取措施防止“猪贱伤农”.
则下个月要采取措施防止“猪贱伤农”.
[数据收集]今年2月-5月玉米、猪肉价格统计表:
月份 | 2 | 3 | 4 | 5 |
玉米价格(元/ |
|
|
|
|
猪肉价格(元/ |
|
|
|
|
[问题解决](1)若今年3月的猪肉价格比上月下降的百分数与5月的猪肉价格比上月下降的百分数相等,求3月的猪肉价格![]() ;
;
(2)若今年6月及以后月份,玉米价格增长的规律不变,而每月的猪内价格按照5月的猪肉价格比上月下降的百分数继续下降,请你预测了月时是否要采取措施防止“碧败伤农”;
(3)若今年6月及以后月份,每月玉米价格增长率是当月猪肉价格增长率的![]() 倍,而每月的猪肉价格增长率都为
倍,而每月的猪肉价格增长率都为![]() .则到7月时只用
.则到7月时只用![]() 元就可以买到
元就可以买到![]() 克猪肉和
克猪肉和![]() 克玉米.请你预测8月时是否要采取措施防止“猪贱伤衣”.
克玉米.请你预测8月时是否要采取措施防止“猪贱伤衣”.