题目内容
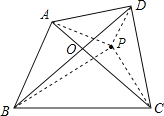
【题目】如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离之和OA+OB+OC+OD最小,并说明你作图的理论依据.

【答案】详见解析.
【解析】
连接AC、BD相交于点O,则点O就是所要找的点;
取不同于点O的任意一点P,连接PA、PB、PC、PD,根据三角形任意两边之和大于第三边可得PA+PC>AC,PB+PD>BD,然后结合图形即可得到PA+PB+PC+PD>OA+OB+OC+OD,从而可得点O就是所要找的四边形ABCD内符合要求的点.
解:要使OA+OB+OC+OD最小,则点O是线段AC、BD的交点.
理由如下:如果存在不同于点O的交点P,连接PA、PB、PC、PD,
那么PA+PC>AC,
即PA+PC>OA+OC,
同理,PB+PD>OB+OD,
∴PA+PB+PC+PD>OA+OB+OC+OD,
即点O是线段AC、BD的交点时,OA+OB+OC+OD之和最小.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目