Question

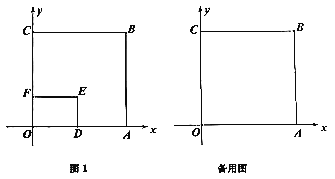
【题目】如图，正方形OABC边长为20，点D的坐标为(,0),且以OD、DE为邻边作长方形ODEF.

(1)请直接写出以下点的坐标:E_____，F______ (用含的式子表示)；

(2)设长方形ODEF与正方形OABC重叠部分面积为S，求S(用含的式子表示)；

(3)S的值能否等于300，若能请求出此时的值；若不能,请说明理由。

Answer 1

【答案】(1)E(m，m)，F(0，m)；(2) 当m20时，S＝m2；当20<m30时，S＝m；当m30时，S＝; (3)能。m=25.

【解析】

（1）利用OD、DE的长，即可得出结论；
（2）分三种情况讨论.OD20；OD>20且D20；D20.画出图形求解.
（3）对（2）中的三种情况逐一令s＝300，求m即可.

解：(1) ∵点D的坐标为(,0),且

∴OD=m, DE=m

∴E(m，m)，F(0，m)

(2)分三种情况.

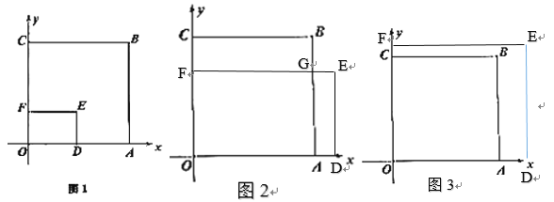
如图1，当OD20即m20时，S=ODDE＝m ＝m2;

如图2，当OD>20且D20即20<m30时，S=OAOF＝20＝m;

如图3，当D20即m30时，S=OAAB＝20＝;

综上所述，当m20时，S＝m2；当20<m30时，S＝m；当m30时，S＝.

(3) 当m20时，S＝m2.当m＝20时S最大＝202= <300,此时m的值不存在；

当20<m30时，S＝m＝300，得m=25，符合题意.

当m30时，S=>300，此时m的值不存在.

综上所述，当m=25时，S＝300.