题目内容
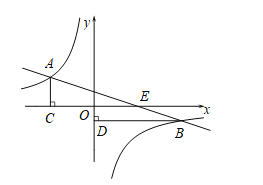
【题目】如图,点A(-3,2)和点B(m,n)在反比例函数y=![]() (k≠0)的图象上(其中m>0),AC⊥x轴,垂足为C,BD⊥y轴,垂足为D,直线AB与x轴相交于点E.
(k≠0)的图象上(其中m>0),AC⊥x轴,垂足为C,BD⊥y轴,垂足为D,直线AB与x轴相交于点E.
(1)写出反比例函数表达式;
(2)求tan∠ABD(用含m的代数式表示);
(3)若CE=6,直接写出B点的坐标.
【答案】(1)![]() ;(2)tan∠ABD=
;(2)tan∠ABD=![]() ;(3)B点的坐标(6,-1).
;(3)B点的坐标(6,-1).
【解析】
(1)直接将点A的横纵坐标分别代入反比例函数解析式即可;
(2)分别延长AC,BD交于点H,根据题意,分别用含m的式子表示点B,点H,再利用三角函数解答即可;
(3)根据题意,可得∠AEC=∠ABD,在△ACE中,利用三角函数求出m的值即可.
(1)∵点A(-3,2)在反比例函数y=![]() (k≠0)的图象上,
(k≠0)的图象上,
∴k=xy=-3×2=-6,
∴反比例函数的解析式为:y=![]() ;
;
(2)分别延长AC,BD交于点H,
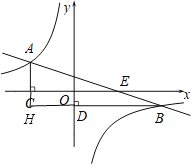
∵点B(m,n)在反比例函数y=![]() 的图象上,
的图象上,
∴点B(m,![]() ),
),
则点H(-3,![]() ),
),
∴AH=2+![]() ,BH=m+3,
,BH=m+3,
∴tan∠ABD=![]() ;
;
(3)∵BD∥x轴,
∴∠AEC=∠ABD,
∴tan∠AEC=![]() ,
,
解得:m=6,
∴点B的坐标为(6,-1).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目