题目内容
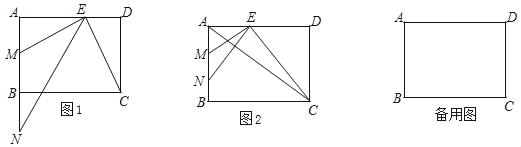
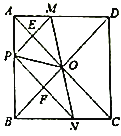
【题目】如图,在正方形![]() 中,点
中,点![]() 是
是![]() 上一动点(不写
上一动点(不写![]() 重合),对角线
重合),对角线![]() 相交于点
相交于点![]() ,过点
,过点![]() 分别作
分别作![]() 的垂线,分别交
的垂线,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,下列结论:①
,下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③
;③![]()
![]()
![]() ;④当
;④当![]()
![]()
![]() 时,点
时,点![]() 是
是![]() 的中点,其中一定正确的结论有_______.(填上所有正确的序号)
的中点,其中一定正确的结论有_______.(填上所有正确的序号)
【答案】①②④
【解析】
①根据正方形的每一条对角线平分一组对角可得∠PAE=∠MAE=45°,然后利用“角边角”证明△APE和△AME全等;②根据全等三角形对应边相等可得PE=EM=![]() PM,同理,FP=FN=
PM,同理,FP=FN=![]() NP,证出四边形PEOF是矩形,得出PF=OE,证得△APE为等腰直角三角形,得出AE=PE,PE+PF=OA,即可得到PM+PN=AC;③判断出△POF不一定等腰直角三角形,△BNF是等腰直角三角形,从而确定出两三角形不一定相似;④证出△APM和△BPN以及△APE、△BPF都是等腰直角三角形,从而得出结论.
NP,证出四边形PEOF是矩形,得出PF=OE,证得△APE为等腰直角三角形,得出AE=PE,PE+PF=OA,即可得到PM+PN=AC;③判断出△POF不一定等腰直角三角形,△BNF是等腰直角三角形,从而确定出两三角形不一定相似;④证出△APM和△BPN以及△APE、△BPF都是等腰直角三角形,从而得出结论.
①∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°,
∵PM⊥AC,
∴∠AEP=∠AEM=90°,
在△APE和△AME中,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴△APE≌△AME(ASA),
故①正确;
②∵△APE≌△AME,
∴PE=EM=![]() PM,
PM,
同理,FP=FN=![]() NP,
NP,
∵正方形ABCD中,AC⊥BD,
又∵PE⊥AC,PF⊥BD,
∴∠PEO=∠EOF=∠PFO=90°,且△APE中AE=PE
∴四边形PEOF是矩形.
∴PF=OE,
∵在△APE中,∠AEP=90°,∠PAE=45°,
∴△APE为等腰直角三角形,
∴AE=PE,
∴PE+PF=OA,
又∵PE=EM=![]() PM,FP=FN=
PM,FP=FN=![]() NP,OA=
NP,OA=![]() AC,
AC,
∴PM+PN=AC,
故②正确;
③∵△APE≌△AME,
∴AP=AM
△BNF是等腰直角三角形,而△POF不一定是,
∴△POF与△BNF不一定相似,
故④错误;
④∵△APE≌△AME,
∴AP=AM,
∴△AMP是等腰直角三角形,
同理,△BPN是等腰直角三角形,
当△PMN∽△AMP时,△PMN是等腰直角三角形.
∴PM=PN,
又∵△AMP和△BPN都是等腰直角三角形,
∴AP=BP,即P是AB的中点,
故④正确;
故答案为①②④.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案【题目】蔬菜基地种植了娃娃菜和油菜两种蔬菜共![]() 亩,设种植娃娃菜
亩,设种植娃娃菜![]() 亩,总收益为
亩,总收益为![]() 万元,有关数据见下表:
万元,有关数据见下表:
成本(单位:万元/亩) | 销售额(单位:万元/亩) | |
娃娃菜 | 2.4 | 3 |
油菜 | 2 | 2.5 |
(1)求![]() 关于
关于![]() 的函数关系式(收益 = 销售额 – 成本);
的函数关系式(收益 = 销售额 – 成本);
(2)若计划投入的总成本不超过![]() 万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
万元,要使获得的总收益最大,基地应种植娃娃菜和油菜各多少亩?
(3)已知娃娃菜每亩地需要化肥![]() kg,油菜每亩地需要化肥
kg,油菜每亩地需要化肥![]() kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的
kg,根据(2)中的种植亩数,基地计划运送所需全部化肥,为了提高效率,实际每次运送化肥的总量是原计划的![]() 倍,结果运送完全部化肥的次数比原计划少
倍,结果运送完全部化肥的次数比原计划少![]() 次,求基地原计划每次运送多少化肥.
次,求基地原计划每次运送多少化肥.