题目内容
近几年,被称为“园林城市,生态家园”的宿迁旅游业得到长足的发展,到宿迁观光旅游的客人越来越多,“真如禅寺”景点每天都吸引大量的游客前来观光.事实表明,如果游客过多,不利于保护珍贵文物,为了实施可持续发展,兼顾社会效益和经济效益,该景点拟采取浮动门票价格的方法来控制游客人数.已知每张门票原价为40元,现设浮动 门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.
门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.
(1)根据图象,求y与x之间的函数关系式;
(2)设该景点一天的门票收入为W元.
①试用x代数式表示W;
②试问:当门票定为多少时,该景点一天的门票收入最高?最高门票收入是多少?
 门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.
门票为每张x元,且40≤x≤70,经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系.(1)根据图象,求y与x之间的函数关系式;
(2)设该景点一天的门票收入为W元.
①试用x代数式表示W;
②试问:当门票定为多少时,该景点一天的门票收入最高?最高门票收入是多少?
(1)设y与x之间的函数关系式为y=kx+b,
根据题意,得
,
解得
.
所以y与x之间的函数关系式为y=-50x+6000;
(2)W=(-50x+6000)x=-50x2+6000x,
当x=-
=60时,W最大,
此时最大值为60×3000=180000(元).
答:该景点门票定为60元时,一天的门票收入最高,最高门票收入是18万元.
根据题意,得
|
解得
|
所以y与x之间的函数关系式为y=-50x+6000;
(2)W=(-50x+6000)x=-50x2+6000x,
当x=-
| 6000 |
| 2×(-50) |
此时最大值为60×3000=180000(元).
答:该景点门票定为60元时,一天的门票收入最高,最高门票收入是18万元.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目




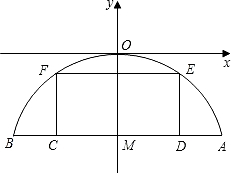 上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.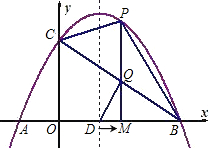 ,求出点Q的坐标,若不存在,说明理由.
,求出点Q的坐标,若不存在,说明理由.