题目内容
【题目】如图，已知，M，N分别为锐角∠AOB的边OA，OB上的点，ON=6，把△OMN沿MN折叠，点O落在点C处，MC与OB交于点P，若MN=MP=5，则PN=( )
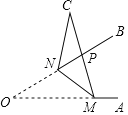
A.2B.3C.
D.
【答案】D
【解析】
根据等边对等角，得出∠MNP=∠MPN，由外角的性质和折叠的性质，进一步证明△CPN∽△CNM，通过三角形相似对应边成比例计算出CP，再次利用相似比即可计算出结果．
解：∵MN=MP，
∴∠MNP=∠MPN，
∴∠CPN=∠ONM，
由折叠可得，∠ONM=∠CNM，CN=ON=6，
∴∠CPN=∠CNM，
又∵∠C=∠C，
∴△CPN∽△CNM，
，即CN2=CP×CM，
∴62=CP×(CP+5)，
解得：CP=4，
又∵
，
∴
，
∴PN=
，
故选：D．
练习册系列答案
相关题目
