Question

【题目】如图，在平行四边形ABCD中，点E在边BC上，连结AE，EM⊥AE，垂足为E，交CD于点M，AF⊥BC，垂足为F，BH⊥AE，垂足为H，交AF于点N，点P显AD上一点，连接CP．

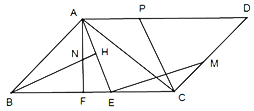
（1）若DP=2AP=4，CP=，CD=5，求△ACD的面积．

（2）若AE=BN，AN=CE，求证：AD=CM+2CE．

Answer 1

【答案】（1）；（2）见解析.

【解析】

（1）作CG⊥AD于G，设PG=x，则DG=4-x，在Rt△PGC和Rt△DGC中，由勾股定理得出方程，解方程得出x=1，即PG=1，得出GC=4，求出AD=6，由三角形面积公式即可得出结果；

（2）连接NE，证明△NBF≌△EAF得出BF=AF，NF=EF，再证明△ANE≌△ECM得出CM=NE，由NF=NE=MC，得出AF=MC+EC，即可得出结论.

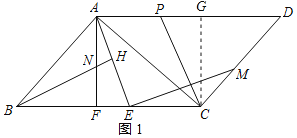
解：（1）解：作CG⊥AD于G，如图1所示：

设PG＝x，则DG＝4﹣x，

在Rt△PGC中，GC2＝CP2﹣PG2＝17﹣x2，

在Rt△DGC中，GC2＝CD2﹣GD2＝52﹣（4﹣x）2＝9+8x﹣x2，

∴17﹣x2＝9+8x﹣x2，

解得：x＝1，即PG＝1，

∴GC＝4，

∵DP＝2AP＝4，

∴AD＝6，

∴S△ACD＝×AD×CG＝×6×4＝12；

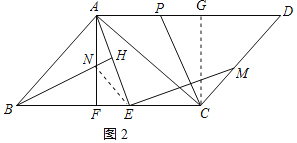
（2）证明：连接NE，如图2所示：

∵AH⊥AE，AF⊥BC，AE⊥EM，

∴∠AEB+∠NBF＝∠AEB+∠EAF＝∠AEB+∠MEC＝90°，

∴∠NBF＝∠EAF＝∠MEC，

在△NBF和△EAF中， ，

∴△NBF≌△EAF（AAS），

∴BF＝AF，NF＝EF，

∴∠ABC＝45°，∠ENF＝45°，FC＝AF＝BF，

∴∠ANE＝∠BCD＝135°，AD＝BC＝2AF，

在△ANE和△ECM中，，

∴△ANE≌△ECM（ASA），

∴CM＝NE，

又∵NF＝NE＝MC，

∴AF＝MC+EC，

∴AD＝MC+2EC．