Question

【题目】图①是一个演讲台，图②是演讲台的侧面示意图，支架BC是一段圆弧，台面与两支架的连接点A，B间的距离为30cm，CD为水平地面，∠ADC＝75°，∠DAB＝60°，BD⊥CD．

（1）求BD的长（结果保留整数，参考数据：sin75°≈0.97，cos75°≈0.26，≈1.7）；

（2）如图③，若圆弧BC所在圆的圆心O在CD的延长线上，且OD＝CD，求支架BC的长（结果保留根号）．

Answer 1

【答案】（1）98cm；（2） cm

【解析】

（1）过点B作BE⊥AD于点E，根据三角函数解答即可；

（2）连接BC，OB，根据等边三角形的判定和弧长公式解答即可．

解：（1）过点B作BE⊥AD于点E，

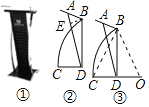
在Rt△ABE中，AB＝30 cm，∠DAB＝60°，

∴BE＝ABsin∠DAB＝30×＝（cm）

∵BD⊥DC，∠ADC＝75°，

∴∠ADB＝15°，

∴∠EBD＝75°．

在Rt△DBE中，BD＝（cm）

（2）连接BC，OB．

∵BD⊥OC，OD＝CD，

∴BC＝OB．

又∵OB＝OC，

∴△OBC是等边三角形，

∴∠BOC＝60°，

∴OB＝（cm），

∴弧BC的长为 ＝（cm）．

∴支架BC的长为 cm