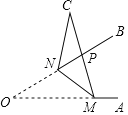
题目内容
【题目】在![]() 中,以
中,以![]() 为斜边,作直角
为斜边,作直角![]() ,使点
,使点![]() 落在
落在![]() 内,
内,![]() .
.
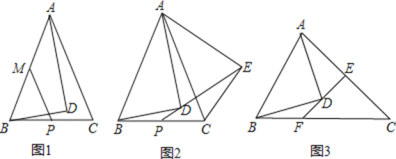
(1)如图1,若![]() ,
,![]() ,
,![]() ,点,
,点,![]() 、
、![]() 分别为
分别为![]() ,
,![]() 的中点,连接
的中点,连接![]() ,求线段
,求线段![]() 的长;
的长;
(2)如图2,若![]() ,把
,把![]() 绕点
绕点![]() 递时针旋转一定角度,得到
递时针旋转一定角度,得到![]() ,连接
,连接![]() 并延长变
并延长变![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)如图3,若![]() ,过点
,过点![]() 的直线交
的直线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,请直接写出线段
,请直接写出线段![]() 、
、![]() 、
、![]() 之间的关系(不需要证明).
之间的关系(不需要证明).
【答案】(1)![]() (2)见解析,(3)
(2)见解析,(3)![]()
【解析】
(1)在直角三角形中,利用锐角三角函数求出AB,得到![]() 利用三角形中位线的性质即可得到答案;
利用三角形中位线的性质即可得到答案;
(2)先利用互余判断出,∠BDP=∠PEC,得到△BDP和△CEQ全等,再用三角形的外角得到∠EPC=∠PQC,即可得到答案;
(3)连接AF,![]() 利用线段垂直平分线上的点到两端点的距离相等,判断出∠AFB=90°,利用勾股定理即可得到答案.
利用线段垂直平分线上的点到两端点的距离相等,判断出∠AFB=90°,利用勾股定理即可得到答案.
解:(1)∵∠ADB=90°,∠BAD=30°,![]() ,
,
∴cos∠BAD![]() ,
,
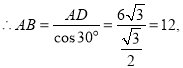
∴AC=AB=12,
∵点P、M分别为BC、AB边的中点,
∴PM=![]() AC=6,
AC=6,
(2)如图2,
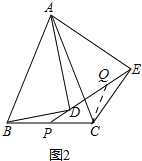
在ED上截取EQ=PD,
∵∠ADB=90°,
∴∠BDP+∠ADE=90°,
∵AD=AE,
∴∠ADE=∠AED,
∵把△ABD绕点A逆时针旋转一定角度,得到△ACE,
∴∠AEC=∠ADB=90°
∵∠AED+∠PEC=90°,
∴∠BDP=∠PEC,
在△BDP和△CEQ中,
 ,
,
∴△BDP≌△CEQ,
∴BP=CQ,∠DBP=∠QCE,
∵∠CPE=∠BDP+∠DBP,
∠PQC=∠PEC+∠QCE,
∴∠EPC=∠PQC,
∴PC=CQ,
∴BP=CP
(3)![]()
理由:如图3,
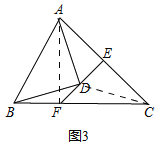
连接AF,![]()
∵EF⊥AC,且AE=EC,
∴FA=FC,∠FAC=∠FCA,
∵EF⊥AC,且AE=EC,
∴∠DAC=∠DCA,DA=DC,
∵AD=BD,
∴BD=DC,
∴∠DBC=∠DCB,
∵∠FAC=∠FCA,∠DAC=∠DCA,
∴∠DAF=∠DCB,
∴∠DAF=∠DBC,
∴∠AFB=∠ADB=90°,
在Rt△ADB中,DA=DB,
∴![]()
在Rt△ABF中,![]()
∵FA=FC
∴![]()

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案