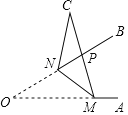
ЬтФПФкШн
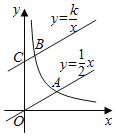
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() НЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЎжБЯп
НЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЎжБЯп![]() ОЙ§ЕуAЃЌCЃЎ
ОЙ§ЕуAЃЌCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛжБЯпACгкЕуMЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
ЂйЕБ![]() ЪЧжБНЧШ§НЧаЮЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЪЧжБНЧШ§НЧаЮЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЂкзїЕуBЙигкЕуCЕФЖдГЦЕу![]() ЃЌдђЦНУцФкДцдкжБЯпlЃЌЪЙЕуMЃЌBЃЌ
ЃЌдђЦНУцФкДцдкжБЯпlЃЌЪЙЕуMЃЌBЃЌ![]() ЕНИУжБЯпЕФОрРыЖМЯрЕШЃЎЕБЕуPдкyжсгвВрЕФХзЮяЯпЩЯЃЌЧвгыЕуBВЛжиКЯЪБЃЌЧыжБНгаДГіжБЯп
ЕНИУжБЯпЕФОрРыЖМЯрЕШЃЎЕБЕуPдкyжсгвВрЕФХзЮяЯпЩЯЃЌЧвгыЕуBВЛжиКЯЪБЃЌЧыжБНгаДГіжБЯп![]() ЕФНтЮіЪНЃЎЃЈkЃЌbПЩгУКЌmЕФЪНзгБэЪОЃЉ
ЕФНтЮіЪНЃЎЃЈkЃЌbПЩгУКЌmЕФЪНзгБэЪОЃЉ
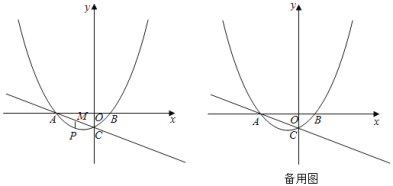
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉЂй
ЃЈ2ЃЉЂй![]() Лђ
Лђ![]() ЃЌЂкжБЯпlЕФНтЮіЪНЮЊ
ЃЌЂкжБЯпlЕФНтЮіЪНЮЊ![]() ,
,![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуAЃЌCЕФзјБъЃЌИљОнЕуAЃЌCЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіЖўДЮКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЂйгЩPMЁЭxжсПЩЕУГіЁЯPMCЁй90ЁуЃЌЗжЁЯMPC=90ЁуМАЁЯPCM=90ЁуСНжжЧщПіПМТЧЃКЃЈiЃЉЕБЁЯMPC=90ЁуЪБЃЌPCЁЮxжсЃЌРћгУЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуPЕФзјБъЃЛЃЈiiЃЉЕБЁЯPCM=90ЁуЪБЃЌЩшPCгыxжсНЛгкЕуDЃЌвзжЄЁїAOCЁзЁїCODЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЧѓГіЕуDЕФзјБъЃЌИљОнЕуCЃЌDЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіжБЯпPCЕФНтЮіЪНЃЌСЊСЂжБЯпPCКЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЧѓГіЕуPЕФзјБъЃЎзлЩЯЃЌДЫЮЪЕУНтЃЛ
ЂкРћгУЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїМАвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЕУГіЕуBЃЌMЕФзјБъЃЌНсКЯЕуCЕФзјБъПЩЕУГіЕуBЁфЕФзјБъЃЌИљОнЕуMЃЌBЃЌBЁфЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЗжБ№ЧѓГіжБЯпBMЃЌBЁфMКЭBBЁфЕФНтЮіЪНЃЌРћгУЦНааЯпЕФаджЪПЩЧѓГіжБЯпlЕФНтЮіЪНЃЎ
НтЃКЃЈ1ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
![]() ЕуCЕФзјБъЮЊ
ЕуCЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
![]() ЕуAЕФзјБъЮЊ
ЕуAЕФзјБъЮЊ![]() ЃЎ
ЃЎ
НЋ![]() ЃЌ
ЃЌ![]() ДњШы
ДњШы![]() ЃЌЕУЃК
ЃЌЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ЃЌ
ЃЌ
![]() ХзЮяЯпЕФНтЮіЪНЮЊ
ХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂй![]() жсЃЌ
жсЃЌ
![]() ЃЌ
ЃЌ
![]() ЗжСНжжЧщПіПМТЧЃЌШчЭМ1ЫљЪОЃЎ
ЗжСНжжЧщПіПМТЧЃЌШчЭМ1ЫљЪОЃЎ
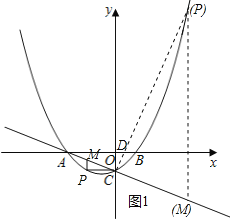
ЃЈiЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() жсЃЌ
жсЃЌ
![]() ЕуPЕФзнзјБъЮЊЉ2ЃЎ
ЕуPЕФзнзјБъЮЊЉ2ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЕуPЕФзјБъЮЊ
ЕуPЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЃЈiiЃЉЕБ![]() ЪБЃЌЩшPCгыxжсНЛгкЕуDЃЎ
ЪБЃЌЩшPCгыxжсНЛгкЕуDЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
гж![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЕуDЕФзјБъЮЊ
ЕуDЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЩшжБЯпPCЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
НЋ![]() ЃЌ
ЃЌ![]() ДњШы
ДњШы![]() ЃЌЕУЃК
ЃЌЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
![]() жБЯпPCЕФНтЮіЪНЮЊ
жБЯпPCЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
СЊСЂжБЯпPCКЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК ЃЌ
ЃЌ
НтЕУЃК ЃЌ
ЃЌ ЃЌ
ЃЌ
ЕуPЕФзјБъЮЊ![]() ЃЎ
ЃЎ
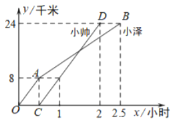
злЩЯЫљЪіЃКЕБ![]() ЪЧжБНЧШ§НЧаЮЪБЃЌЕуPЕФзјБъЮЊ
ЪЧжБНЧШ§НЧаЮЪБЃЌЕуPЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЂкЕБy=0ЪБЃЌ![]() ,
,
НтЕУЃКx1=-4ЃЌx2=2ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЎ
ЁпЕуCЕФзјБъЮЊЃЈ0ЃЌ-2ЃЉЃЌЕуBЃЌBЁфЙигкЕуCЖдГЦЃЌ
ЁрЕуBЁфЕФзјБъЮЊЃЈ-2ЃЌ-4ЃЉЃЎ
ЁпЕуPЕФКсзјБъЮЊmЃЈmЃО0ЧвmЁй2ЃЉЃЌ
ЁрЕуMЕФзјБъЮЊ![]() ,
,
РћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіЃКжБЯпBMЕФНтЮіЪНЮЊ![]() ЃЌжБЯпBЁфMЕФНтЮіЪНЮЊ
ЃЌжБЯпBЁфMЕФНтЮіЪНЮЊ![]() ЃЌжБЯпBBЁфЕФНтЮіЪНЮЊy=x-2ЃЎ
ЃЌжБЯпBBЁфЕФНтЮіЪНЮЊy=x-2ЃЎ
ЗжШ§жжЧщПіПМТЧЃЌШчЭМ2ЫљЪОЃК
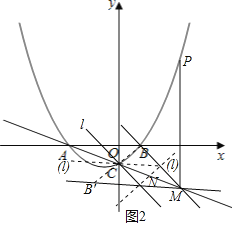
ЕБжБЯпlЁЮBMЧвЙ§ЕуCЪБЃЌжБЯпlЕФНтЮіЪНЮЊ![]() ,
,
ЕБжБЯпlЁЮBЁфMЧвЙ§ЕуCЪБЃЌжБЯпlЕФНтЮіЪНЮЊ![]() ,
,
ЕБжБЯпlЁЮBBЁфЧвЙ§ЯпЖЮCMЕФжаЕу![]() ЪБЃЌжБЯпlЕФНтЮіЪНЮЊ
ЪБЃЌжБЯпlЕФНтЮіЪНЮЊ![]() ,
,
злЩЯЫљЪіЃКжБЯпlЕФНтЮіЪНЮЊ![]() ,
,![]() Лђ
Лђ![]() .
.

 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
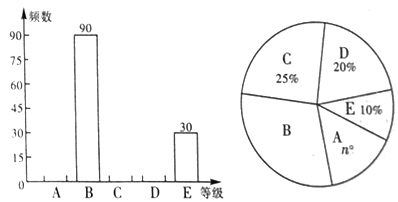
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИЁОЬтФПЁПФГаЃЦпФъМЖ6ИіАрЕФ180УћбЇЩњМДНЋВЮМгББОЉЪажабЇЩњПЊЗХадПЦбЇЪЕМљЛюЖЏЫЭПЮЕНаЃПЮГЬЕФбЇЯАЃЎбЇЯАФкШнАќРЈвдЯТ7ИіСьгђЃКAЃЎздШЛгыЛЗОГЃЌBЃЎНЁПЕгыАВШЋЃЌCЃЎНсЙЙгыЛњаЕЃЌDЃЎЕчзггыПижЦЃЌEЃЎЪ§ОнгыаХЯЂЃЌFЃЎФмдДгыВФСЯЃЌGЃЎШЫЮФгыРњЪЗЃЎЮЊСЫНтбЇЩњЯВЛЖЕФПЮГЬСьгђЃЌбЇЩњЛсПЊеЙСЫвЛДЮЕїВщбаОПЃЌЧыНЋЯТУцЕФЙ§ГЬВЙШЋЃЎ
ЪеМЏЪ§ОнбЇЩњЛсМЦЛЎЕїВщ30УћбЇЩњЯВЛЖЕФПЮГЬСьгђзїЮЊбљБОЃЌЯТУцГщбљЕїВщЕФЖдЯѓбЁдёКЯРэЕФЪЧЁЁЁЁЃЛЃЈЬюађКХЃЉ
ЂйбЁдёЦпФъМЖ1АрЁЂ2АрИї15УћбЇЩњзїЮЊЕїВщЖдЯѓ
ЂкбЁдёЛњЦїШЫЩчЭХЕФ30УћбЇЩњзїЮЊЕїВщЖдЯѓ
ЂлбЁдёИїАрбЇКХЮЊ6ЕФБЖЪ§ЕФ30УћбЇЩњзїЮЊЕїВщЖдЯѓ
ЕїВщЖдЯѓШЗЖЈКѓЃЌЕїВщаЁзщЛёЕУСЫ30УћбЇЩњЯВЛЖЕФПЮГЬСьгђШчЯТЃК
AЃЌCЃЌDЃЌDЃЌGЃЌGЃЌFЃЌEЃЌBЃЌGЃЌ
CЃЌCЃЌGЃЌDЃЌBЃЌAЃЌGЃЌFЃЌFЃЌAЃЌ
GЃЌBЃЌFЃЌGЃЌEЃЌGЃЌAЃЌBЃЌGЃЌG
ећРэЁЂУшЪіЪ§ОнећРэЁЂУшЪібљБОЪ§ОнЃЌЛцжЦЭГМЦЭМБэШчЯТЃЌЧыВЙШЋЭГМЦБэКЭЭГМЦЭМЃЎ
ФГаЃЦпФъМЖбЇЩњЯВЛЖЕФПЮГЬСьгђЭГМЦБэ
ПЮГЬСьгђ | ШЫЪ§ |
A | 4 |
B | 4 |
C | 3 |
D | 3 |
E | 2 |
F | ЁЁ4ЁЁ |
G | ЁЁ10ЁЁ |
КЯМЦ | 30 |
ЗжЮіЪ§ОнЁЂЭЦЖЯНсТлЧыФуИљОнЩЯЪіЕїВщНсЙћЯђбЇаЃЭЦМіБОДЮЫЭПЮЕНаЃЕФПЮГЬСьгђЃЌФуЕФЭЦМіЪЧЁЁЁЁЃЈЬюAЉGЕФзжФИДњКХЃЉЃЌЙРМЦШЋФъМЖДѓдМгаЁЁЁЁУћбЇЩњЯВЛЖетИіПЮГЬСьгђЃЎ