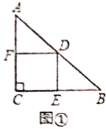题目内容
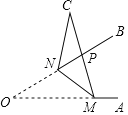
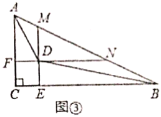
【题目】如图,矩形![]() 的对角线交于点
的对角线交于点![]() .点
.点![]() 在
在![]() 边上,
边上,![]() 连结
连结![]() 交对角线
交对角线![]() 于点
于点![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .
.
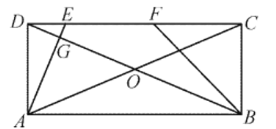
(1)求证:![]() .
.
(2)判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)若![]() 和
和![]() 面积分别为
面积分别为![]() 和
和![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)见解析;(2)![]() ,理由见解析;(3)最大值为1
,理由见解析;(3)最大值为1
【解析】
(1)根据矩形性质可知![]() 为等腰三角形,从而可得
为等腰三角形,从而可得![]() ,进而得出
,进而得出![]() ;即得
;即得![]() ;
;
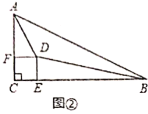
(2)连结![]() ,由矩形性质可知O是AC的中点,从而可得OF是
,由矩形性质可知O是AC的中点,从而可得OF是![]() 的中位线,得出
的中位线,得出![]() ,结合(1)的结论可知OF是DB的垂直平分线,故DF=BF;
,结合(1)的结论可知OF是DB的垂直平分线,故DF=BF;
(3)由![]() 可设
可设![]() ,由
,由![]() 可将图形中线段CE、EF、DF都用
可将图形中线段CE、EF、DF都用![]() 的代数式表示,从而表示出
的代数式表示,从而表示出![]() ,然后计算比值,根据K的取值范围确定最大值即可.
,然后计算比值,根据K的取值范围确定最大值即可.
![]() 已知矩形
已知矩形![]() ,
,
∴OA=OB,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() 连结
连结![]() ,
,
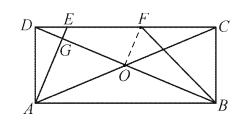
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 设
设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
![]() ,
,
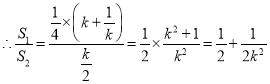 ,
,
![]() ,
,
![]() 当
当![]() 时,
时,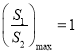 .
.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目