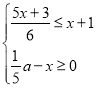ћвƒњƒЏ»Ё
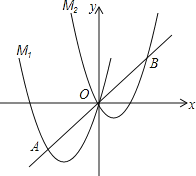
°Њћвƒњ°њ“—÷™Їѓ эy=y1+y2£ђ∆д÷–y1”лx≥…Јі±»јэ£ђy2”лx©Б2≥…’э±»јэ£ђЇѓ эµƒ„‘±дЅњxµƒ»°÷µЈґќІ «x![]() £ђ«“µ±x=1їтx=4 ±£ђyµƒ÷µЊщќ™
£ђ«“µ±x=1їтx=4 ±£ђyµƒ÷µЊщќ™![]() £Ѓ
£Ѓ
«лґ‘Є√Їѓ эЉ∞∆дЌЉѕуљш––»зѕ¬ћљЊњ£Ї
£®1£©љвќц љћљЊњ£ЇЄщЊЁЄшґ®µƒћхЉю£ђњ…“‘»Јґ®≥цЄ√Їѓ эµƒљвќц љќ™£Ї°° °°£Ѓ
£®2£©Їѓ эЌЉѕућљЊњ£Ї
ҐўЄщЊЁљвќц љ£ђ≤є»Ђѕ¬±н£Ї
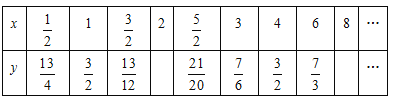
ҐЏЄщЊЁ±н÷– эЊЁ£ђ‘Џ»зЌЉЋщ Њµƒ∆љ√ж÷±љ«„ш±кѕµ÷–√иµг£ђ≤Ґї≠≥цЇѓ эЌЉѕу
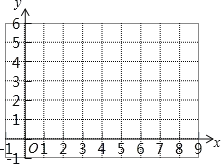
£®3£©љбЇѕї≠≥цµƒЇѓ эЌЉѕу£ђљвЊцќ ћв£Ї
Ґўµ±x![]() £ђ
£ђ![]() £ђ8 ±£ђЇѓ э÷µЈ÷±рќ™y1£ђy2£ђy3£ђ‘тy1£ђy2£ђy3µƒіу–°єЎѕµќ™£Ї°° °°£ї£®”√°∞£Љ°±їт°∞=°±±н Њ£©
£ђ8 ±£ђЇѓ э÷µЈ÷±рќ™y1£ђy2£ђy3£ђ‘тy1£ђy2£ђy3µƒіу–°єЎѕµќ™£Ї°° °°£ї£®”√°∞£Љ°±їт°∞=°±±н Њ£©
ҐЏ»ф÷±ѕяy=k”лЄ√Їѓ эЌЉѕу”–ЅљЄцљїµг£ђ‘тkµƒ»°÷µЈґќІ «°° °°£ђіЋ ±£ђxµƒ»°÷µЈґќІ «°° °°£Ѓ
°Њір∞Є°њ£®1£©![]() £ї£®2£©Ґўір∞ЄЉыљвќц£їҐЏір∞ЄЉыљвќц£ї£®3£©Ґўy2£Љy1£Љy3£їҐЏ1£Љk
£ї£®2£©Ґўір∞ЄЉыљвќц£їҐЏір∞ЄЉыљвќц£ї£®3£©Ґўy2£Љy1£Љy3£їҐЏ1£Љk![]() £ђ
£ђ![]() x£Љ2їт2£Љx°№8£Ѓ
x£Љ2їт2£Љx°№8£Ѓ
°Њљвќц°њ
£®1£©”√іэґ®ѕµ эЈ®…и![]() £ђy2=k2£®x-2£©£ђ‘т
£ђy2=k2£®x-2£©£ђ‘т![]() +k2(x2)£ђљЂ“—÷™ћхЉюіъ»лµ√єЎ”Џk1°Ґk2Јљ≥ћ„й£ђЉіњ…«уµ√Є√Їѓ эљвќц љ£ї
+k2(x2)£ђљЂ“—÷™ћхЉюіъ»лµ√єЎ”Џk1°Ґk2Јљ≥ћ„й£ђЉіњ…«уµ√Є√Їѓ эљвќц љ£ї
£®2£©—°»° µ± э÷µћо±н£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–√иµг£ђ”√∆љїђ«ъѕяі”„уµљ”“Ћ≥іќЅђљ”Єчµг£ђї≠≥цЌЉѕу£ї
£®3£©єџ≤мЌЉѕу£ђµ√≥цљб¬џ£Ѓ
£®1£©…и![]() £ђy2=k2£®x©Б2£©£ђ‘т
£ђy2=k2£®x©Б2£©£ђ‘т![]() £ђ
£ђ
”…ћв“вµ√£Ї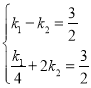 £ђ
£ђ
љвµ√£Ї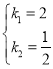 £ђ
£ђ
°аЄ√Їѓ эљвќц љќ™![]() £Ѓ
£Ѓ
є ір∞Єќ™£Ї![]() £ђ
£ђ
£®2£©ҐўЄщЊЁљвќц љ£ђ
µ±x=2 ±£ђ![]() £ї
£ї
µ±x=8 ±£ђ![]() £ї
£ї
≤є»Ђѕ¬±н£Ї

ҐЏЄщЊЁ…ѕ±н‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–√иµг£ђї≠≥цЌЉѕу£Ѓ
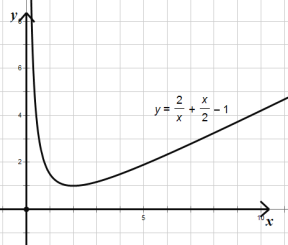
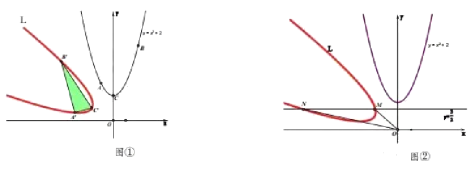
£®3£©Ґў”…£®2£©÷–ЌЉѕуњ…µ√£Ї£®2£ђ1£© «ЌЉѕу…ѕ„оµЌµг£ђ‘ЏЄ√µг„у≤а£ђyЋжx‘ціуґшЉх–°£ї‘ЏЄ√µг”“≤аyЋжx‘ціуґш‘ціу£ђ
°яµ±x![]() £ђ
£ђ![]() £ђ8 ±£ђґ‘”¶µƒЇѓ э÷µЈ÷±рќ™y1£ђy2£ђy3£ђ
£ђ8 ±£ђґ‘”¶µƒЇѓ э÷µЈ÷±рќ™y1£ђy2£ђy3£ђ
°а![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
°аy2£Љy1£Љy3£Ѓ є ір∞Єќ™£Їy2£Љy1£Љy3£Ѓ ҐЏєџ≤мЌЉѕуµ√£Їx °аµ±÷±ѕяy=k”лЄ√ЌЉѕу”–ЅљЄцљїµг ±£ђ1£Љk іЋ ±xµƒЈґќІ «£Ї є ір∞Єќ™£Ї1£Љk![]() £ђЌЉѕу„оµЌµгќ™£®2£ђ1£©£ђ
£ђЌЉѕу„оµЌµгќ™£®2£ђ1£©£ђ![]() £ђ
£ђ![]() x£Љ2їт2£Љx°№8£Ѓ
x£Љ2їт2£Љx°№8£Ѓ![]() £ђ
£ђ![]() x£Љ2їт2£Љx°№8£Ѓ
x£Љ2їт2£Љx°№8£Ѓ

 ћф’љ100µ•‘™Љм≤в ‘ЊнѕµЅ–ір∞Є
ћф’љ100µ•‘™Љм≤в ‘ЊнѕµЅ–ір∞Є