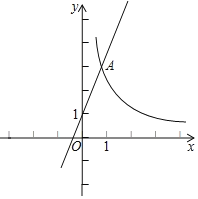题目内容
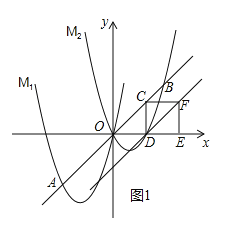
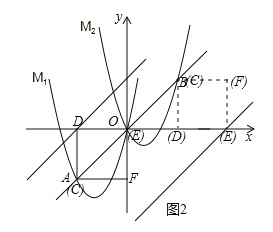
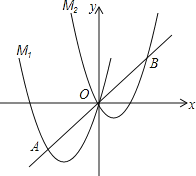
【题目】如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是﹣3.
(1)求a的值及M2的表达式;
(2)点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.
①当点C的横坐标为2时,直线y=x+n恰好经过正方形CDEF的顶点F,求此时n的值;
②在点C的运动过程中,若直线y=x+n与正方形CDEF始终没有公共点,求n的取值范围(直接写出结果).
【答案】(1)M2的顶点为(1,﹣1),M2的表达式为y=x2﹣2x;(2)①n=﹣2;②n>3,n<﹣6.
【解析】
(1)将点A横坐标代入y=x,即可得出点A纵坐标,从而得出点A的坐标,根据点A在抛物线M1:y=ax2+4x上,代入即可得出a的值,将抛物线M1化为顶点式,根据平移的原则即可得出抛物线M2;
(2)①把点C横坐标代入y=x,即可得出点C坐标,从而得出点F坐标,把点F代入y=x+n即可得出n的值;
②根据直线y=x+n与正方形CDEF始终没有公共点,直接可得出n的取值范围.
(1)∵点A在直线y=x,且点A的横坐标是﹣3,
∴A(﹣3,﹣3),
把A(﹣3,﹣3)代入y=ax2+4x,
解得a=1,
∴M1:y=x2+4x,顶点为(﹣2,﹣4),
∴M2的顶点为(1,﹣1),
∴M2的表达式为y=x2﹣2x;
(2)①由题意,C(2,2),
∴F(4,2),
∵直线y=x+n经过点F,
∴2=4+n,
解得n=﹣2;
②将y=x代入y=x2﹣2x,得
x2﹣2x=x,解得:x1=0,x2=3,
∴点B(3,3),
当点C与点A重合时,点D的坐标为(-3,0),
此时有-3+n=0,解得:n=3;
当点C与点B重合时,点E的坐标为(6,0),
此时有6+n=0,解得:n=-6,
综上可知,当直线y=x+n与正方形CDEF始终没有公共点时,n>3或n<﹣6.