题目内容
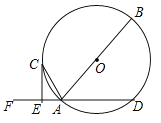
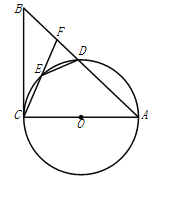
【题目】如图,△ABC中,BC=4,⊙P与△ABC的边或边的延长线相切.若⊙P半径为2,△ABC的面积为5,则△ABC的周长为( )
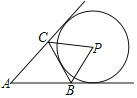
A.8B.10C.13D.14
【答案】C
【解析】
根据三角形的面积公式以及切线长定理即可求出答案.
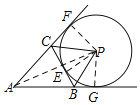
连接PE、PF、PG,AP,
由题意可知:∠PEC=∠PFA=PGA=90°,
∴S△PBC=![]() BCPE=
BCPE=![]() ×4×2=4,
×4×2=4,
∴由切线长定理可知:S△PFC+S△PBG=S△PBC=4,
∴S四边形AFPG=S△ABC+S△PFC+S△PBG+S△PBC=5+4+4=13,
∴由切线长定理可知:S△APG=![]() S四边形AFPG=
S四边形AFPG=![]() ,
,
∴![]() =
=![]() ×AGPG,
×AGPG,
∴AG=![]() ,
,
由切线长定理可知:CE=CF,BE=BG,
∴△ABC的周长为AC+AB+CE+BE
=AC+AB+CF+BG
=AF+AG
=2AG
=13,
故选C.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目