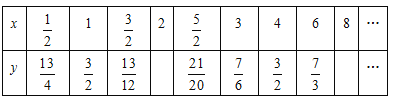
题目内容

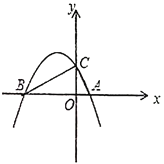
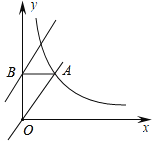
【题目】如图，正比例函数y＝kx与反比例函数y＝的图象有一个交点A（m，4），AB⊥y轴于点B，平移直线y＝kx，使其经过点B，得到直线l，则直线l对应的函数表达式是_____．

【答案】y＝x+4

【解析】

由点A在反比例函数图象上可求得m的值，进而可求得k的值，易求点B坐标，然后根据直线平移前后k相等，且平移后过点B即得答案．

解：∵正比例函数y＝kx与反比例函数y＝的图象有一个交点A（m，4），

∴4m＝23，解得：m＝，故A（，4），

则4＝k，解得：k＝，故正比例函数解析式为：y＝x，

∵AB⊥y轴于点B，∴B（0，4），

∵平移直线y＝x，使其经过点B（0，4），∴平移后的直线解析式为：y＝x+4．

故答案为：y＝x+4．

练习册系列答案
相关题目

【题目】如图，在四边形ABCD中，∠A＝∠B＝90°，AB＝6，AD＝1，BC＝2，P为AB边上的动点，当△PAD与△PBC相似时，PA＝_____．

【题目】随着科技的进步和网络资源的丰富，在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论.为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图.

根据图中信息，解答下列问题：

（1）求本次调查的学生总人数，并补全条形统计图；

（2）求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

（3）该校共有学生人，请你估计该校对在线阅读最感兴趣的学生人数.

【题目】如图，抛物线经过点，点，交轴于点，连接，.

（1）求抛物线的解析式；

（2）点为抛物线第二象限上一点，满足，求点的坐标；

（3）将直线绕点顺时针旋转，与抛物线交于另一点，求点的坐标.

【题目】已知函数y=y1+y2，其中y1与x成反比例，y2与x﹣2成正比例，函数的自变量x的取值范围是x，且当x=1或x=4时，y的值均为．

请对该函数及其图象进行如下探究：

（1）解析式探究：根据给定的条件，可以确定出该函数的解析式为：　 　．

（2）函数图象探究：

①根据解析式，补全下表：

②根据表中数据，在如图所示的平面直角坐标系中描点，并画出函数图象

（3）结合画出的函数图象，解决问题：

①当x，，8时，函数值分别为y1，y2，y3，则y1，y2，y3的大小关系为：　 　；（用“＜”或“=”表示）

②若直线y=k与该函数图象有两个交点，则k的取值范围是　 　，此时，x的取值范围是　 　．

【题目】已知等腰△ABC中，AB＝AC，∠FDE的顶点D在线段BC上，不与B、C重合．

（1）如图①，若DE∥AC，DF∥AB且点D在BC中点时，四边形AEDF是什么四边形并证明？

（2）将∠EDF绕点D旋转至如图②所示位置，若∠B＝∠C＝∠EDF＝α，BD＝m，CD＝n，设△BDE的面积为S1，△CDF的面积为S2，求S1S2的值．（用含有m、n、α的代数式表示）

（3）将∠EDF绕点D旋转至如图③所示位置，连接EF，若∠B＝∠C＝∠EDF，且EF垂直平分AD，BD＝m，CD＝n，则的值为多少？（要有解答过程）．

【题目】如图，在正方形中，是边的中点，将沿折叠，使点落在点处，的延长线与边交于点.下列四个结论:①;②;③;④S正方形ABCD，其中正确结论的个数为（ ）

A.个B.个C.个D.个

【题目】某学校从甲、乙两名班主任中选拔一名参加教育局组织的班主任技能比赛，选拔内容分案例分析、班会设计、才艺展示三个项目，选拔比赛结束后，统计这两位班主任成绩并制成了如图所示的条形统计图：

（1）乙班班主任三个项目的成绩中位数是 ；

（2）用6张相同的卡片分别写上甲、乙两名班主任的六项成绩，洗匀后，从中任意抽取一张，求抽到的卡片写有“80”的概率；

（3）若按照图12所示的权重比进行计算，选拔分数最高的一名班主任参加比赛，应确定哪名班主任获得参赛资格，说明理由．

【题目】在一个不透明的盒子里装有5个分别写有数字0，1，2，3，4的小球，它们除数字不同外其余全部相同.现从盒子里随机摸出一个小球（不放回），设该小球上的数字为m，再从盒子中摸出一个小球，设该小球上的数字为n，点P的坐标为，则点P落在抛物线与x轴所围成的区域内（含边界）的概率是________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网