题目内容
【题目】已知抛物线y＝x2+bx+c经过点A（2，﹣3）．
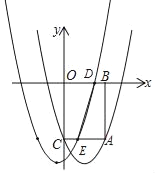
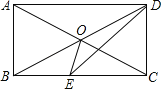
（1）如图，过点A分别向x轴，y轴作垂线，垂足分别为B，C，得到矩形ABOC，且抛物线经过点C．
①求抛物线的解析式．
②将抛物线向左平移m（m＞0）个单位，分别交线段OB，AC于D，E两点．若直线DE刚好平分矩形ABOC的面积，求m的值．
（2）将抛物线平移，使点A的对应点为A1（2﹣n，3b），其中n≥1．若平移后的抛物线仍然经过点A，求平移后的抛物线顶点所能达到最高点时的坐标．
【答案】（1）①y＝x2﹣2x﹣3；②m＝
；（2）顶点坐标（0，﹣7）．
【解析】
（1）①将A（2，﹣3），B（2，0）代入y＝x2+bx+c即可求出；
②因为直线DE刚好平分矩形ABOC的面积，所以AE＝OD＝m，DB＝CE＝2﹣m，D（m，0），E（2﹣m，﹣3），易知F（3，0），所以DF＝3﹣m，于是3﹣m＝m，从而求出m；
（2）由抛物线y＝x2+bx+c经过点A（2，﹣3），可得y＝x2+bx﹣2b﹣7，由A的对应点为A1（2﹣n，3b），可知抛物线向左平移了n个单位，向上平移（3b+3）个单位，则平移后y＝（x+n）2+b（x+n）﹣2b﹣7+3b+3，整理后根据平移后的抛物线仍然经过点A（2，﹣3），继而可求得b＝﹣n﹣1，进而可求得顶点坐标.
（1）①∵四边形ABOC是矩形，A（2，﹣3），
∴B（2，0），C（0．﹣3），
∵抛物线y＝x2+bx+c过点A、C，
∴
， 解得：
，
∴抛物线解析式为y＝x2﹣2x﹣3；
②如图，设原抛物线与x轴正半轴交于点F，
∵直线DE刚好平分矩形ABOC的面积，
∴AE＝OD＝m，DB＝CE＝2﹣m
∴D（m，0），E（2﹣m，﹣3）
∵易知F（3，0），
∴DF＝3﹣m，
∵DF＝AE，
∴3﹣m＝m，
∴m＝；
（2）抛物线y＝x2+bx+c经过点A（2，﹣3）．
﹣3＝22+2b+c，
∴c＝﹣2b﹣7，
∴y＝x2+bx﹣2b﹣7，
∵A的对应点为A1（2﹣n，3b），
∴抛物线向左平移了n个单位，向上平移（3b+3）个单位
则平移后y＝（x+n）2+b（x+n）﹣2b﹣7+3b+3，
整理得y＝（x+n）2+b（x+n）+b﹣4＝（x+n+
）2﹣
+b﹣4，
∵平移后的抛物线仍然经过点A（2，﹣3），
∴﹣3＝（2+n）2+b（2+n）+b﹣4，
∴n2+4n+3+b（3+n）＝0，
∴（n+1（n+3））+b（n+3）＝0，
（
∵n≥1，∴n+3>0，
∴n+1+b＝0，b＝﹣n﹣1，
顶点坐标（﹣n﹣，﹣ +b﹣4），
y顶＝﹣+b﹣4＝﹣
（b﹣2）2﹣3＝﹣（n+3）2﹣3，
∵n≥1，-＜0，
∴n＝1时，顶点最高，此时b＝﹣1﹣1＝﹣2，
顶点坐标（0，﹣7）．
