题目内容
【题目】定义:有一组对角互补的四边形叫做互补四边形.
![]() 概念理解:
概念理解:
①在互补四边形![]() 中,
中,![]() 与
与![]() 是一组对角,若
是一组对角,若![]() 则
则![]() _
_ ![]()
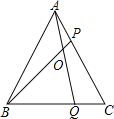
②如图1,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,且
上,且![]() 求证:四边形
求证:四边形![]() 是互补四边形.
是互补四边形.
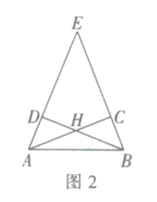
![]() 探究发现:如图2,在等腰
探究发现:如图2,在等腰![]() 中,
中,![]() 点
点![]() 分别在边
分别在边![]() 上,
上, ![]() 四边形
四边形![]() 是互补四边形,求证:
是互补四边形,求证:![]() .
.
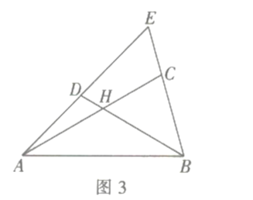
![]() 推广运用:如图3,在
推广运用:如图3,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,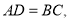 四边形
四边形![]() 是互补四边形,若
是互补四边形,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)①90;②见解析;(2)见解析;(3)![]() .
.
【解析】
(1)①由互补四边形和四边形内角和定理即可求出∠A的度数;
②证明![]() 得
得![]() ,进而可得
,进而可得![]() ,从而可证明四边形
,从而可证明四边形![]() 是互补四边形;
是互补四边形;
(2)先证明![]() 得
得![]() ,根据EA=EB可得
,根据EA=EB可得![]() ,根据三角形内角和定理得∠AHB=180°-(
,根据三角形内角和定理得∠AHB=180°-(![]() ),再根据互补四边形的定义可得结论;
),再根据互补四边形的定义可得结论;
(3)如图,作![]() 于点
于点![]() 交
交![]() 的延长线于点
的延长线于点![]() 则
则![]() ,由四边形CEDH是互补四边形可得
,由四边形CEDH是互补四边形可得![]() ,进而证明
,进而证明![]() ,
,![]() ,求得
,求得![]() ,再证明
,再证明![]() 即可得到结论.
即可得到结论.
(1)①解:∵四边形ABCD是互补四边形,
∴∠B+∠D=180°,
∵∠B:∠C:∠D=2:3:4,
∴∠B=60°,∠C=90°,
又∵∠A+∠B+∠C+∠D=360°,
∴∠A=180°-∠C=90°;
故答案为:90;
②证明:![]()
![]()
又![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是互补四边形.
是互补四边形.
![]() 证明:
证明:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是互补四边形,
是互补四边形,![]()
![]()
![]()
![]() 如图,作
如图,作![]() 于点
于点![]() 交
交![]() 的延长线于点
的延长线于点![]()
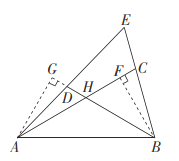
则![]()
![]() 四边形
四边形![]() 是互补四边形,
是互补四边形,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
在![]() 中,
中,![]()
![]() 设
设![]() 则
则![]()
![]()
![]()
![]()
![]() .
.
![]() ,
,
![]()
![]()

练习册系列答案
相关题目
【题目】疫情无情人有情,爱心捐款传真情.疫情期间,某企业员工积极参加献爱心活动,该企业率先捐款的50名员工的捐款情况统计如下表:
金额/元 | 50 | 100 | 200 | 500 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的平均数、中位数、众数分别是( )
A.276,100,200B.276,200,100C.370,100,100D.370,200,100