题目内容
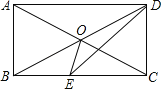
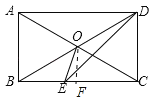
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
【答案】(1)详见解析;(2)1
【解析】
(1)证出∠BAD=∠BCD,得出四边形ABCD是平行四边形,得出OA=OC,OB=OD,证出AC=BD,即可解决问题;
(2)作OF⊥BC于F.求出EC、OF即可解决问题;
(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形.
(2)解:作OF⊥BC于F,如图所示.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=![]() CD=1,
CD=1,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△OEC的面积=![]() ECOF=1.
ECOF=1.

练习册系列答案
相关题目