题目内容
【题目】在平直角坐标系中,规定:抛物线![]()
![]() 的相关直线为
的相关直线为![]() .例如:二次函数
.例如:二次函数![]() 的相关直线为
的相关直线为![]() .
.

(1)直接写出抛物线![]() 的相关直线,并求出抛物线
的相关直线,并求出抛物线![]() 与其相关直线的交点坐标;
与其相关直线的交点坐标;
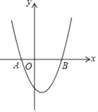
(2)如图,抛物线![]()
![]() 与它的相关直线
与它的相关直线![]() 交于
交于![]() 、
、![]() 两点.
两点.
①求抛物线的解析式;
②连结![]() ,求
,求![]() 的面积;
的面积;
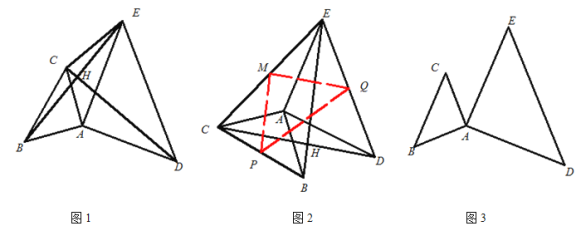
③作![]() ,过抛物线上一动点
,过抛物线上一动点![]() (不与
(不与![]() 、
、![]() 重合)作直线
重合)作直线![]() 的平行线交
的平行线交![]() 于点
于点![]() ,若以点
,若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,直接写出点
为顶点的四边形是平行四边形,直接写出点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ,交点坐标为
,交点坐标为![]() ,
,![]() ;(2)①
;(2)①![]() ;②10;③
;②10;③![]() ,
,![]()
【解析】
(1)根据原文所给的概念直接写出抛物线![]() 的相关直线,然后联立二者得到方程组,最后求出方程组的解即可;
的相关直线,然后联立二者得到方程组,最后求出方程组的解即可;
(2)①根据相关直线的概念结合题意直接得出![]() ,
,![]() ,然后将点B的坐标代入求得
,然后将点B的坐标代入求得![]() ,由此即可得出该抛物线的解析式;②首先根据抛物线解析式求出对称轴,从而得出点A坐标,最后根据三角形面积公式进一步计算即可;③首先根据题意得出AB=4,然后利用等腰三角形性质得知点M在AB的垂直平分线上,由此进一步求解得出点M坐标为(3,2),然后设点P坐标为(
,由此即可得出该抛物线的解析式;②首先根据抛物线解析式求出对称轴,从而得出点A坐标,最后根据三角形面积公式进一步计算即可;③首先根据题意得出AB=4,然后利用等腰三角形性质得知点M在AB的垂直平分线上,由此进一步求解得出点M坐标为(3,2),然后设点P坐标为(![]() ,
,![]() ),点Q坐标为(
),点Q坐标为(![]() ,
,![]() ),最后根据平移的性质列出相应的方程组加以分析求解即可.
),最后根据平移的性质列出相应的方程组加以分析求解即可.
(1)∵抛物线![]()
![]() 的相关直线为
的相关直线为![]() ,
,
∴![]() 的相关直线为:
的相关直线为:![]() ,
,
联立二者可得:![]() ,
,
解得:![]() 或
或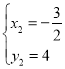 ,
,
∴交点坐标为(0,1),(![]() ,4);
,4);
(2)①由题意得:![]() ,
,![]() ,
,
∵点![]() 在
在![]() 上,点B横坐标为0,
上,点B横坐标为0,
∴点B坐标为(5,0),
∵抛物线过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴抛物线的解析式为![]() ;
;
②∵抛物线解析式为:![]() ,
,
∴该抛物线对称轴为:![]() ,
,
∵点B坐标为(5,0),
∴点![]() 坐标为(1,0),
坐标为(1,0),
∴![]() ;
;
③∵点A坐标为(1,0),点B坐标为(5,0),点C坐标为(0,5),
∴AB=4,∠ABC=45°,
∵AM⊥BC,
∴△ABM为等腰直角三角形,
∴点M在AB的垂直平分线上,
∴点M的横坐标为1+2=3,
由此将横坐标3代入![]() 可得:
可得:![]() ,
,
∴点M坐标为(3,2),
设点P坐标为(![]() ,
,![]() ),点Q坐标为(
),点Q坐标为(![]() ,
,![]() ),
),
根据平移的性质可得:
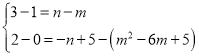 或
或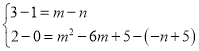 ,
,
解得:![]() (舍去),
(舍去),![]() 或
或![]()
综上所述,点P的横坐标为:![]() ,
,![]() .
.

【题目】疫情无情人有情,爱心捐款传真情.疫情期间,某企业员工积极参加献爱心活动,该企业率先捐款的50名员工的捐款情况统计如下表:
金额/元 | 50 | 100 | 200 | 500 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的平均数、中位数、众数分别是( )
A.276,100,200B.276,200,100C.370,100,100D.370,200,100