题目内容
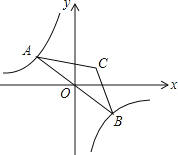
【题目】如图,已知反比例函数y=﹣![]() 的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为__.
的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为__.
【答案】y=![]()
【解析】
连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,证明△AOD∽△OCE,根据相似三角形的性质求出△AOD和△OCE面积比,根据反比例函数图象上点的特征求出△AOD面积,即可得到△EOC面积,根据反比例函数比例系数k的几何意义求解.
解:连接CO,过点A作AD⊥x轴于点D,过点C作CE⊥x轴于点E,

∵反比例函数y=![]() 的图象与直线y=kx(k<0)相交于点A、B,△ABC是以AB为底作的等腰三角形,∠ACB=120°,
的图象与直线y=kx(k<0)相交于点A、B,△ABC是以AB为底作的等腰三角形,∠ACB=120°,
∴CO⊥AB,∠CAB=30°,
则∠AOD+∠COE=90°,
∵∠DAO+∠AOD=90°,
∴∠DAO=∠COE,
又∵∠ADO=∠CEO=90°,
∴△AOD∽△OCE,
∴![]() =tan60°=
=tan60°=![]() ,
,
∴![]()
∵点A是双曲线y=![]() 在第二象限分支上的一个动点,
在第二象限分支上的一个动点,
∴S△AOD=![]() =
=![]()
∴S△OCE=![]() ,即
,即![]() ×OE×CE=
×OE×CE=![]() ,
,
∴OE×CE=![]() ,
,
∴这个图象所对应的函数解析式为y=![]() .
.
故答案为:y=![]() .
.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
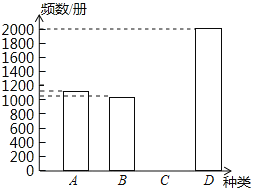
名牌中学课时作业系列答案【题目】在学校开展的“献爱心”活动中,小东同学打算在暑假期间帮助一家社会福利书店推销A、B、C、D四种书刊.为了了解四种书刊的销售情况,小东对五月份这四种书刊的销售量进行了统计,小东通过采集数据,绘制了两幅不完整的统计图表(如图),请你根据所给出的信息解答以下问题:
书刊种类 | 频数 | 频率 |
A |
| 0.25 |
B | 1000 | 0.20 |
C | 750 | 0.15 |
D | 2000 |
|
(1)填充频率分布表中的空格及补全频数分布直方图;
(2)若该书店计划定购此四种书刊6000册,请你计算B种书刊应采购多少册较合适?
(3)针对调查结果,请你帮助小东同学给该书店提一条合理化的建议.