题目内容
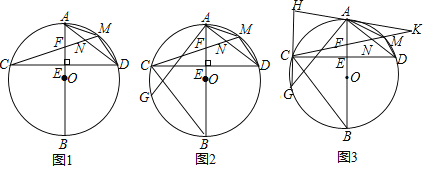
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆O交AC于点D,交BC于点E,以点B为顶点作∠CBF,使得∠CBF=![]() ∠BAC,交AC延长线于点F连接BD、AE,延长AE交BF于点G,
∠BAC,交AC延长线于点F连接BD、AE,延长AE交BF于点G,
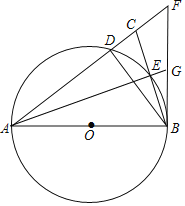
(1)求证:BF为⊙O的切线;(2)求证:ACBC=BDAG;(3)若BC=2![]() ,CD:CF=4:5,求⊙O的半径.
,CD:CF=4:5,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)⊙O的半径OA=5.
【解析】
(1)由圆周角定理得出∠AEB=∠ADB=90°,得出AE⊥BC,由等腰三角形的性质得出∠BAE=∠CAE=![]() ∠BAC,证出∠BAE=∠CBF,证出∠ABF=90°,得出BF⊥OB,即可得出结论;
∠BAC,证出∠BAE=∠CBF,证出∠ABF=90°,得出BF⊥OB,即可得出结论;
(2)证出∠DBC=∠BAE,证明△BDC∽△ABG,得出![]() ,即可得出结论;
,即可得出结论;
(3)由(2)得:∠DBC=∠CBF,由角平分线性质得出![]() ,设BD=4x,则BF=5x,由勾股定理得:DF=
,设BD=4x,则BF=5x,由勾股定理得:DF=![]() =3x,证明△ABD∽△BFD,得出
=3x,证明△ABD∽△BFD,得出![]() ,求出AB=
,求出AB=![]() x,AD=
x,AD=![]() x,得出CD=AC﹣AD=
x,得出CD=AC﹣AD=![]() x,在Rt△BDC中,由勾股定理得出方程,解方程得x=
x,在Rt△BDC中,由勾股定理得出方程,解方程得x=![]() ,得出AB=10,即可得出⊙O的半径.
,得出AB=10,即可得出⊙O的半径.
(1)证明:∵AB是⊙O的直径,
∴∠AEB=∠ADB=90°,
∴AE⊥BC,∠ABE+∠BAE=90°,
∵AB=AC,
∴∠BAE=∠CAE=![]() ∠BAC,
∠BAC,
∵∠CBF=![]() ∠BAC,
∠BAC,
∴∠BAE=∠CBF,
∴∠ABE+∠CBF=90°,
∴∠ABF=90°,
∴BF⊥OB,
∴BF为⊙O的切线;
(2)证明:∵∠DBC=∠CAE,∠BAE=∠CAE,
∴∠DBC=∠BAE,
∵∠BDC=90°=∠ABG,
∴△BDC∽△ABG,
∴![]() ,
,
∴ABBC=BDAG,
∵AB=AC,
∴ACBC=BDAG;
(3)解:由(2)得:∠DBC=∠CBF,
∴![]() ,
,
设BD=4x,则BF=5x,
由勾股定理得:DF=![]() =
=
∵∠BAD+∠ABD=90°,∠BAD+∠F=90°,
∴∠ABD=∠F,
∵∠ADB=∠BDF=90°,
∴△ABD∽△BFD,
∴![]() ,即
,即![]() ,
,
解得:AB=![]() x,AD=
x,AD=![]() x,
x,
∴AC=AB=![]() x,
x,
∴CD=AC﹣AD=![]() x,
x,
在Rt△BDC中,由勾股定理得:(4x)2+(![]() x)2=(2
x)2=(2![]() )2,
)2,
解得:x=![]() ,
,
∴AB![]() x=10,
x=10,
∴⊙O的半径OA=5.