Question

【题目】△ABC中，AB＝AC，∠ABC＝72°，以B为圆心，以任意长为半径画弧，分别交BA、BC于M、N，再分别以M、N为圆心，以大于MN为半径画弧，两弧交于点P，射线BP交AC于点D，则图中与BC相等的线段有（　　）

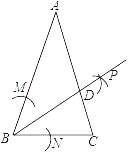
A. BDB. CDC. BD和ADD. CD和AD

Answer 1

【答案】C

【解析】

由基本作图得到BP平分∠ABC，所以∠ABP=∠CBP=36°，则利用等腰三角形的性质得∠C=∠ABC=72°，再利用三角形内角和定理计算出∠A=36°，于是得到AD=BD，然后计算出∠BDC=72°，从而得到∠BDC=∠C，所以BD=BC.

解：由画法得BP平分∠ABC，则∠ABP＝∠CBP＝ ，

∵AB＝AC，

∴∠C＝∠ABC＝72°，

∴∠A＝180°﹣2×72°＝36°，

∴∠A＝∠ABD，

∴AD＝BD，

∵∠BDC＝∠A+∠ABD＝72°，

∴∠BDC＝∠C，

∴BD＝BC，

即BC＝BD＝AD．

故选：C．