Question

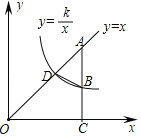
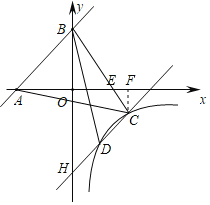
【题目】如图所示，一次函数y＝x+3与x轴、y轴分别交于点A、B，将直线AB向下平移与反比例函数（x＞0）交于点C、D，连接BC交x轴于点E，连接AC，已知BE＝3CE，且S△ACE＝．

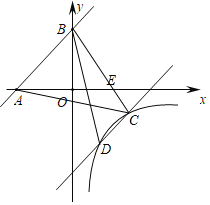
（1）求直线BC和反比例函数解析式；（2）连接BD，求△BCD的面积．

Answer 1

【答案】（1） ， ；（2）S△BCD＝ .

【解析】

（1）作CF⊥x轴于F，根据BE＝3CE，且S△ACE＝ 求得S△ABE＝ ，根据三角形面积求得AE，从而求得OE和CF，由三角形相似求得EF，得到C点的坐标，即可根据勾股定理求得BC，根据反比例函数图象上点的坐标特征求得反比例函数的解析式；

（2）设直线CD的解析式为y＝x+b，令直线CD交y轴于H，根据待定系数法求得解析式，从而求得H点的坐标，联立方程求得D点的坐标，然后根据S△BCD＝S△BCH﹣S△BDH求得即可．

（1）作CF⊥x轴于F，

由直线y＝x+3可知，A（﹣3，0），B（0，3），

∵BE＝3CE，且S△ACE＝，

∴S△ABE＝，

∴ AEOB＝，即AE3＝，

∴AE＝，

∴OE＝，

∵S△ACE＝AECF＝，

∴CF＝1，

∵CF∥OB，

∴△ECF∽△EBO，

∴，即 ＝，

∴EF＝，

∴OF＝OE+DF＝2，

∴C（2，﹣1），

∴BC＝，

∵反比例函数y＝ （x＞0）经过点C，

∴m＝2×（﹣1）＝﹣2，

∴反比例函数解析式为y＝﹣ ；

（2）∵将直线AB向下平移与反比例函数y＝（x＞0）交于点C、D，

∴设直线CD的解析式为y＝x+b，令直线CD交y轴于H，

把C（2，﹣1）代入得，﹣1＝2+b，

∴b＝﹣3，

∴直线CD的解析式为y＝x﹣3，

∴H（0，﹣3），

解，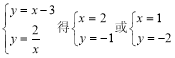

∴D（1，﹣2），

∴S△BCD＝S△BCH﹣S△BDH＝ ×3×2﹣×3×1＝．