题目内容
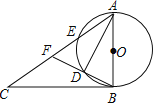
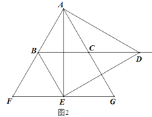
【题目】如图①,已知Rt△ABC中,∠ACB=90°,AC=8,AB=10,点D是AC边上一点(不与C重合),以AD为直径作⊙O,过C作CE切⊙O于E,交AB于F.
(1)若⊙O半径为2,求线段CE的长;
(2)若AF=BF,求⊙O的半径;
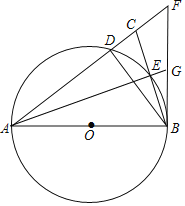
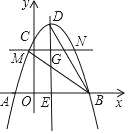
(3)如图②,若CE=CB,点B关于AC的对称点为点G,试求G、E两点之间的距离.

【答案】(1)CE=4![]() ;(2)⊙O的半径为3;(3)G、E两点之间的距离为9.6
;(2)⊙O的半径为3;(3)G、E两点之间的距离为9.6
【解析】
(1)根据切线的性质得出∠OEC=90°,然后根据勾股定理即可求得;
(2)由勾股定理求得BC,然后通过证得△OEC∽△BCA,得到![]() ,即
,即![]() 解得即可;
解得即可;
(3)证得D和M重合,E和F重合后,通过证得△GBE∽△ABC,![]() ,即
,即![]() ,解得即可.
,解得即可.
解:(1)如图①,连接OE,
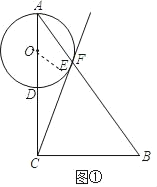
∵CE切⊙O于E,
∴∠OEC=90°,
∵AC=8,⊙O的半径为2,
∴OC=6,OE=2,
∴CE=![]() ;
;
(2)设⊙O的半径为r,
在Rt△ABC中,∠ACB=90°,AB=10,AC=8,
∴BC=![]() =6,
=6,
∵AF=BF,
∴AF=CF=BF,
∴∠ACF=∠CAF,
∵CE切⊙O于E,
∴∠OEC=90°,
∴∠OEC=∠ACB,
∴△OEC∽△BCA,
∴![]() ,即
,即![]()
解得r=3,
∴⊙O的半径为3;
(3)如图②,连接BG,OE,设EG交AC于点M,
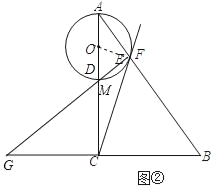
由对称性可知,CB=CG,
∵CE=CG,
∴∠EGC=∠GEC,
∵CE切⊙O于E,
∴∠GEC+∠OEG=90°,
∵∠EGC+∠GMC=90°,
∴∠OEG=∠GMC,
∵∠GMC=∠OME,
∴∠OEG=∠OME,
∴OM=OE,
∴点M和点D重合,
∴G、D、E三点在同一直线上,
连接AE、BE,
∵AD是直径,
∴∠AED=90°,即∠AEG=90°,
又CE=CB=CG,
∴∠BEG=90°,
∴∠AEB=∠AEG+∠BEG=180°,
∴A、E、B三点在同一条直线上,
∴E、F两点重合,
∵∠GEB=∠ACB=90°,∠B=∠B,
∴△GBE∽△ABC,
∴![]() ,即
,即![]()
∴GE=9.6,
故G、E两点之间的距离为9.6.

 阅读快车系列答案
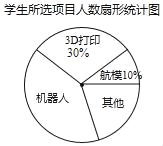
阅读快车系列答案【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m=_____,n=_____;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为_____°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.