题目内容
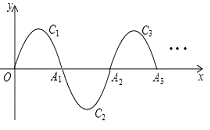
【题目】如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，直至得到C2018，若点P（4035，m）在第2018段抛物线C2018上，则m的值是( )
A.1B.－1C.0D.4035
【答案】B
【解析】
根据题意可以发现题目中各个点的变化规律，从而可以求得m的值，本题得以解决．
∵y=-x（x-2）（0≤x≤2），
∴配方可得y=-（x-1）2+1（0≤x≤2），
∴顶点坐标为（1，1），
∴A1坐标为（2，0）
∵C2由C1旋转得到，
∴OA1=A1A2，即C2顶点坐标为（3，-1），A2（4，0）；
将C2绕点A2旋转180°得C3，交x轴于点A3；
…
∴P（4035，m）在抛物线C2018上，
∵n=2018是偶数，
∴P（4035，m）在x轴的下方，m=-1，
∴当x=4035时，m=-1．
故选：B．
练习册系列答案
相关题目
