题目内容
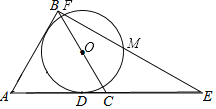
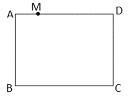
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的一点,且
边上的一点,且![]() ,点
,点![]() 在矩形
在矩形![]() 所在的平面中,且
所在的平面中,且![]() ,则
,则![]() 的最大值是_________.
的最大值是_________.
【答案】5+![]() .
.
【解析】
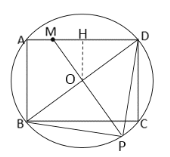
由四边形是矩形得到内接于![]() ,利用勾股定理求出直径BD的长,由
,利用勾股定理求出直径BD的长,由![]() 确定点P在
确定点P在![]() 上,连接MO并延长,交
上,连接MO并延长,交![]() 于一点即为点P,此时PM最长,利用勾股定理求出OM,再加上OP即可得到PM的最大值.
于一点即为点P,此时PM最长,利用勾股定理求出OM,再加上OP即可得到PM的最大值.
连接BD,
∵四边形ABCD是矩形,
∴∠BAD=∠BCD=90![]() ,AD=BC=8,
,AD=BC=8,
∴BD=10,
以BD的中点O为圆心5为半径作![]() ,
,
∵![]() ,
,
∴点P在![]() 上,
上,
连接MO并延长,交![]() 于一点即为点P,此时PM最长,且OP=5,
于一点即为点P,此时PM最长,且OP=5,
过点O作OH⊥AD于点H,
∴AH=![]() AD=4,
AD=4,
∵AM=2,
∴MH=2,
∵点O、H分别为BD、AD的中点,
∴OH为△ABD的中位线,
∴OH=![]() AB=3,
AB=3,
∴OM=![]() ,
,
∴PM=OP+OM=5+![]() .
.
故答案为:5+![]() .
.

练习册系列答案
相关题目