题目内容
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求抛物线的函数表达式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一动点,求
上方抛物线上的一动点,求![]() 面积
面积![]() 的最大值并求出此时点
的最大值并求出此时点![]() 的坐标;
的坐标;
(3)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,连接
,连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的一个夹角等于
的一个夹角等于![]() 的3倍时,请直接写出点
的3倍时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,点
,点![]() 坐标为
坐标为![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() ,
, ![]()
【解析】
(1)利用B(5,0)用待定系数法求抛物线解析式;
(2)作PQ∥y轴交BC于Q,根据![]() 求解即可;
求解即可;
(3)作∠CAN=∠NAM1=∠ACB,则∠A M1B=3∠ACB, 则![]() NAM1∽
NAM1∽![]() A C M1,通过相似的性质来求点M1的坐标;作AD⊥BC于D,作M1关于AD的对称点M2, 则∠A M2C=3∠ACB,根据对称点坐标特点可求M2的坐标.
A C M1,通过相似的性质来求点M1的坐标;作AD⊥BC于D,作M1关于AD的对称点M2, 则∠A M2C=3∠ACB,根据对称点坐标特点可求M2的坐标.
(1)把![]() 代入
代入![]() 得
得
![]()
![]() .
.
∴![]() ;
;
(2)作PQ∥y轴交BC于Q,设点![]() ,则
,则
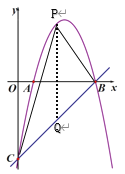
∵![]()
∴OB=5,
∵Q在BC上,
∴Q的坐标为(x,x-5),
∴PQ=![]() =
=![]() ,
,
∴![]()
=
=![]()
∴当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ,
,
∴点![]() 坐标为
坐标为![]() .
.
(3)如图1,作∠CAN=∠NAM1=∠ACB,则∠A M1B=3∠ACB,
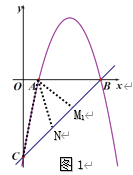
∵∠CAN=∠NAM1,
∴AN=CN,
∵![]() =-(x-1)(x-5),
=-(x-1)(x-5),
∴A的坐标为(1,0),C的坐标为(0,-5),
设N的坐标为(a,a-5),则
∴![]() ,
,
∴a= ![]() ,
,
∴N的坐标为(![]() ,
,![]() ),
),
∴AN2=![]() =
=![]() ,AC2=26,
,AC2=26,
∴![]() ,
,
∵∠NAM1=∠ACB,∠N M1A=∠C M1A,
∴![]() NAM1∽
NAM1∽![]() A C M1,
A C M1,
∴![]() ,
,
∴![]() ,
,
设M1的坐标为(b,b-5),则
∴![]() ,
,
∴b1= ![]() ,b2=6(不合题意,舍去),
,b2=6(不合题意,舍去),
∴M1的坐标为![]() ,
,
如图2,作AD⊥BC于D,作M1关于AD的对称点M2, 则∠A M2C=3∠ACB,
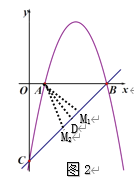
易知![]() ADB是等腰直角三角形,可得点D的坐标是(3,-2),
ADB是等腰直角三角形,可得点D的坐标是(3,-2),
∴M2 横坐标= ![]() ,
,
M2 纵坐标= ![]() ,
,
∴M2 的坐标是![]() ,
,
综上所述,点M的坐标是![]() 或
或![]() .
.