Question

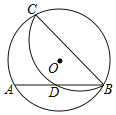
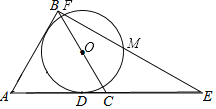
【题目】如图，△ABC为等边三角形，O为BC的中点，作⊙O与AC相切于点D．

（1）求证：AB与⊙O相切；

（2）延长AC到E，使得CE＝AC，连接BE交⊙O与点F、M，若AB＝4，求FM的长．

Answer 1

【答案】（1）见解析；（2）2

【解析】

（1）连接OD，作OG⊥AB于G，由等边三角形的性质得出∠OCD＝∠OBG＝∠ABC＝60°，由切线的性质得出∠ODC＝90°＝∠OGB，证明△OBG≌△OCD得出OG＝OD，即可得出结论；

（2）连接OA、OM，作OH⊥FM于H，由垂径定理得出FH＝MH，证明四边形OHBG是矩形，得出OH＝BG，由直角三角形的性质得出OH＝BG＝OB＝1，OG＝BG＝，在Rt△OMH中，由勾股定理得出MH＝＝，即可得出结果．

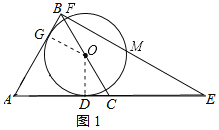
（1）证明：连接OD，作OG⊥AB于G，如图1所示：

则∠OGB＝90°，

∵△ABC为等边三角形，

∴∠OCD＝∠OBG＝∠ABC＝60°，

∵O为BC的中点，

∴OB＝OC，

∵⊙O与AC相切于点D，

∴AC⊥OD，

∴∠ODC＝90°＝∠OGB，

在△OBG和△OCD中，

，

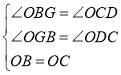∴△OBG≌△OCD（AAS），

∴OG＝OD，

∴AB与⊙O相切；

（2）解：连接OA、OM，作OH⊥FM于H，如图2所示：

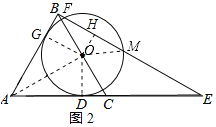
则∠OHB＝90°，FH＝MH，

∵CE＝AC，AC＝BC，

∴CE＝BC，

∴∠CBE＝∠CEB＝∠ACB＝30°，

∴∠ABE＝∠ABC+∠CBE＝90°，

∵∠OGB＝90°，

∴四边形OHBG是矩形，

∴OH＝BG，

∵△ABC是等边三角形，O为BC的中点，

∴OB＝BC＝AB＝2，

∵∠BOG＝90°﹣60°＝30°，

∴OH＝BG＝OB＝1，OG＝BG＝，

在Rt△OMH中，OM＝OG＝，OH＝1，

∴MH＝＝，

∴FM＝2MH＝2．