题目内容
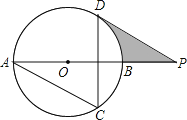
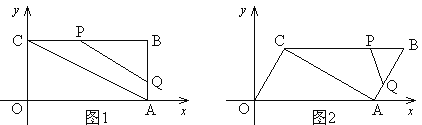
【题目】在平面直角坐标系中,O为原点,四边形OABC的顶点A在![]() 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
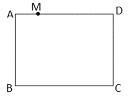
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
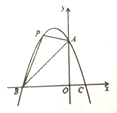
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥![]() 轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F.若B1E: B1F=1:3,点B1的横坐标为![]() ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出![]() 的取值范围.
的取值范围.
【答案】B(4,2);![]() (3,0);
(3,0);![]() ≤m≤1+
≤m≤1+![]() 或
或![]() ≤m≤3.
≤m≤3.
【解析】
根据矩形的性质得出点B的坐标;过点P作PD⊥OA,垂足为点D,点B关于PQ的对称点为![]() ,从而得出△P
,从而得出△P![]() D∽△
D∽△![]() QA,即
QA,即![]() =2则
=2则![]() A=1,得出O
A=1,得出O![]() =3,即得出点
=3,即得出点![]() 的坐标;根据平行四边形的慈宁宫中得出OA=4,OC=2,OC⊥AC,得出点
的坐标;根据平行四边形的慈宁宫中得出OA=4,OC=2,OC⊥AC,得出点![]() 不与点E,F重合,也不在线段EF的延长线上,然后分点
不与点E,F重合,也不在线段EF的延长线上,然后分点![]() 在线段EF的延长线上和点
在线段EF的延长线上和点![]() 在线段EF(除点E,F)上两种情况分别进行计算,根据题意得出点
在线段EF(除点E,F)上两种情况分别进行计算,根据题意得出点![]() 的横坐标为m,根据比值得出
的横坐标为m,根据比值得出![]() G=m,设OG=a,从而得出GF和OF的长度,然后根据线段之间的关系得出a的值,从而求出m的取值范围.
G=m,设OG=a,从而得出GF和OF的长度,然后根据线段之间的关系得出a的值,从而求出m的取值范围.
(1)①∵OA=4,OC=2,
∴点B的坐标为(4,2);
②如图1,过点P作PD⊥OA,垂足为点D
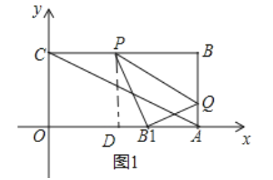
∵BQ:BP=1:2
点B关于PQ的对称点为![]()
∴![]() Q:
Q:![]() P=1:2
P=1:2
∵∠PD![]() =∠P
=∠P![]() Q=∠
Q=∠![]() AQ=90°
AQ=90°
∴∠P![]() D=∠
D=∠![]() QA
QA
∴△P![]() D∽△
D∽△![]() QA
QA
∴![]() =2
=2
∴![]() A=1 ∴O
A=1 ∴O![]() =3
=3
即点![]() (3,0).
(3,0).
(2)∵四边形OABC为平行四边形 OA=4,OC=2,且OC⊥AC
∴∠OAC=30°
∵![]() E:
E:![]() F=1:3
F=1:3
∴点![]() 不与点E,F重合,也不在线段EF的延长线上
不与点E,F重合,也不在线段EF的延长线上
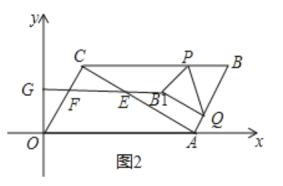
①当点![]() 在线段EF的延长线上时,如图2,延长
在线段EF的延长线上时,如图2,延长![]() F与y轴交于点G,点
F与y轴交于点G,点![]() 的横坐标为m,
的横坐标为m,![]() F∥x轴
F∥x轴
![]() E:
E:![]() F=1:3
F=1:3
∴![]() G=m
G=m
设OG=a 则GF=![]() ,OF=
,OF=![]()
∴![]() G=
G=![]() E+EF+FG=(2-
E+EF+FG=(2-![]() )+(4-
)+(4-![]() )+
)+![]() =m
=m
∴a=-![]()
即![]() 的纵坐标为-
的纵坐标为-![]()
m的取值范围是![]() ≤m≤1+
≤m≤1+![]() .
.
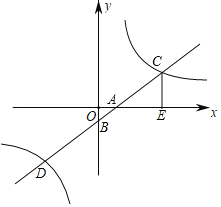
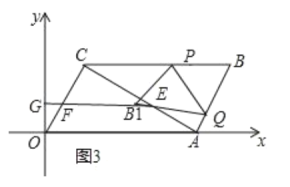
②当点![]() 在线段EF(除点E,F)上时,如图3,延长
在线段EF(除点E,F)上时,如图3,延长![]() F与y轴交于点G,点
F与y轴交于点G,点![]() 的横坐标为m
的横坐标为m
![]() F∥x轴,
F∥x轴,![]() E:
E:![]() F=1:3 ∴
F=1:3 ∴![]() G=m 设OG=a 则 GF=
G=m 设OG=a 则 GF=![]() ,OF=
,OF=![]()
∴CF=2-![]() ∴FE=4-
∴FE=4-![]()
![]() F=
F=![]() EF=3-
EF=3-![]() a
a
∴![]() G=
G=![]() F+FG=(3-
F+FG=(3-![]() )a+
)a+![]() a=m
a=m
∴a=-![]() 即点
即点![]() 的纵坐标为-
的纵坐标为-![]()
M的取值范围是![]() ≤m≤3
≤m≤3