Question

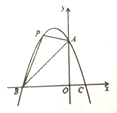
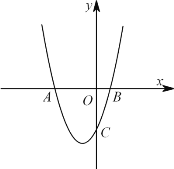
【题目】如图，抛物线与轴交于、两点，与轴交于点．

（1）求点、、的坐标；

（2）若点在轴的上方，以、、为顶点的三角形与全等，平移这条抛物线，使平移后的抛物线经过点与点，请你写出平移过程，并说明理由。

Answer 1

【答案】（1），，；（2），.理由见解析.

【解析】

（1）令中y=0，求出点A、B的坐标，令x=0即可求出点C的坐标；

（2）分两种全等情况求出点D的坐标，再设平移后的解析式，将点B、D的坐标代入即可求出解析式，由平移前的解析式根据顶点式的数值变化得到平移的方向与距离.

（1）令中y=0，得，

解得： ，

∴，.

当中x=0时，y=-3，

∴.

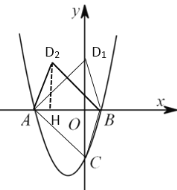
（2）当△ABD1≌△ABC时，

∵，

∴由轴对称得D1（0,3），

设平移后的函数解析式为，将点B、D1的坐标代入，得

，解得，

∴平移后的解析式为，

∵平移前的解析式为，

∴将向右平移3个单位，再向上3个单位得到；

当△ABD2≌△BAC时，即△ABD2≌△BAD1，

作D2H⊥AB，

∴AH=OB=1，D2H=OD1=3，

∴OH=OA-AH=3-1=2，

∴D2(-2，3),

设平移后的解析式为，将点B、D2的坐标代入得

，解得，

∴平移后的函数解析式为，

∵平移前的解析式为，

∴将向右平移1个单位，再向上平移3个单位得到.