Question

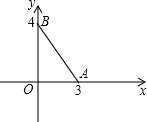
如图，在直角坐标系中，点A、B的坐标分别是（3，0）、（0，4），Rt△ABO内心的坐标是（　　）

A．（ 7 2 ， 7 2 ）

B．（ 3 2 ，2）

C．（1，1）

D．（ 3 2 ，1）

Answer 1

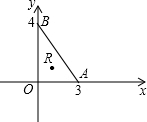
设△OAB的内切圆半径为R；
∵A（3，0），B（0，4），
∴OA=3，OB=4；
Rt△OAB中，由勾股定理得：AB=

OA2+OB2

=5，
∴R=

1

2

（OA+OB-AB）=1；
所以Rt△OAB的内心坐标为（1，1），故选C．