题目内容
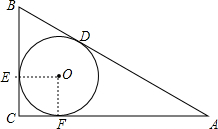
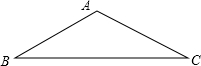
如图，在△ABC中，∠C=90°，BC=3，AC=4，内切圆半径是______，外接圆半径______．
连接OB，CO，AO，
∵∠C=90°，BC=3，AC=4，
∴BA=
=5，
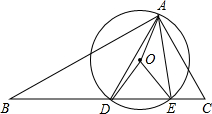
∴其外接圆的半径为2.5．
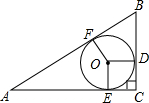
设△ABC的内切圆⊙O半径是r，连接OA、OB、OC、OD、OE、OF，切点是D、E、F，
则OD⊥AC，OE⊥BC，OF⊥AB，OD=OE=OF=r，
∵AC=4，BC=3，AB=5，
根据三角形的面积公式得：S△ACB=S△OAC+S△OBC+S△OAB，
∴AC×BC=AC×r+BC×r+AB×r，即：3×4=3r+4r+5r，
∴r=1．
故答案为：1，2.5．
∵∠C=90°，BC=3，AC=4，
∴BA=
| 32+42 |
∴其外接圆的半径为2.5．
设△ABC的内切圆⊙O半径是r，连接OA、OB、OC、OD、OE、OF，切点是D、E、F，
则OD⊥AC，OE⊥BC，OF⊥AB，OD=OE=OF=r，
∵AC=4，BC=3，AB=5，
根据三角形的面积公式得：S△ACB=S△OAC+S△OBC+S△OAB，
∴AC×BC=AC×r+BC×r+AB×r，即：3×4=3r+4r+5r，
∴r=1．
故答案为：1，2.5．
练习册系列答案
计算高手系列答案
相关题目
